Глава 6

 

                   Мировое древо,

         «карта мира»  и  Откровение от Иоанна

 

 

         У лукоморья дуб зелёный

                                                                                                                              А.С. Пушкин

 

Нет ничего более действенного, чем стебли тысячелистника и панцирь черепахи

                                                                                                                              Прилагаемые суждения[1]

 

                                                                                               Дерево, высокое и крепкое, найдёт свой топор

                                                                                                                              Дао дэ цзин, 76

 

Праформу религий справедливо угадывают в шаманизме, а когда шаман отправляется в путешествие, он восходит на крону Мирового дерева. Три яруса древа простираются на три мира: корни его достигают преисподней, могучие ветви проникают во все стороны света, а верхушка теряется в бес­предельном. Норны поливают  корни,  три парки под ветвями прядут нити судьбы, на ветвях поют три вещие птицы, а  ствол  обвивает дракон  – он же   хранитель Древа.

Дерево представляют и Человеком с раски­нутыми руками, из волос, костей, органов и чле­нов которого создан мир; либо Бог сам бывает подвешен на древе как  жертва  во  искупление греха мира.

Шаманское число Дерева – девять или три­жды три: девять миров дол­жен посетить шаман, проходя по кроне‚ - девять кругов, девять сфер и де­вять областей мы обнаруживаем повсюду как священную Эннеаду или абсолютную Полноту (плерому). Это же древо есть  Ficus religiosа‚  и  оно стало  первоначальным  храмом:   ранние  алтари человечества сооружались  просто под  священным деревом‚  а последним  алтарём стал сам Просветлённый.

 

«Числа древа три и девять  исторически предшествуют  семи», - 

 

сви­детельствует  Мирча Элиаде[2].

Символ полноты содержит в себе все сим­волы,  перетекающие друг в друга и сливаю­щиеся в Едином символе; фиксация тех или иных значений, частных аспектов Символа – задача реформаторов и основателей религий, - но то уже яблоко, похищенное у дракона.

Число – одно из сечений символа;  числа имеют свою мистерию, и на­чало их теряется во тьме. Ключом к хорошо сберегаемым сокровищам ка­жутся они одним, оракулом либо шифром, посредством которых  незримое обращается к нам - представляются  другим, но в любом случае язык  чисел уходит в корни  вещей.

 

Такова‚ в частно­сти‚ эннеада - девятка,  сумма трёх первых уровней Октавы: 1+3+5. Уникальность Мирового древа в том, что оно выступает связующим звеном между Небом и  преисподней, то есть являет собою разворачивающуюся структуру, содержащую потенции эволюции.

 

Первое известное упоминание о «Девяти полях» или «Девяти залах» находится в трак­тате II века до н.э. в Китае, но происхождение их, по-видимому, куда более раннее. Поля были нане­сены на карту и получили обозна­чения; древ­нейшее  наименование   их - Ло шу, или «Карта феи реки Ло» - Фиг. 6.1.:

 

        Из Жёлтой реки вышла Таблица,

        Из реки Ло вышли Письмена.

                                              Мудрые следуют этому

                                              («Прилагаемые суждения», 11).

 

         С той поры без девяти полей не обходятся китайская астрология и геоман­тия – фэншуй. По системе девяти залов и пяти начал гадали на пан­цире черепахи.

После того‚ что было сказано‚ не будет неожиданностью встречать далее де­вятку во всё новом и новом обличье.

         Детальное рассмотрение непременно опять приведёт нас к Октаве, пока же всмотримся пристальнее в эту «детскую забаву» - магический квадрат трёх. «Жемчужиной и самым древним из экспонатов комбинаторной кунтскамеры» назвал его Мартин Гарднер[3].

         Первые девять чисел натураль­ного ряда размещены в квадрате 3х3 таким способом, что образуют одинаковую сумму‚ равную 15, при сложении их по строкам, по столбцам  и по диагоналям. Заметим также, что суммы чисел по углам квадрата (8+4+2+6) и «по кресту» (3+9+7+1) равны и составляют двадцать;  сумма малого квадрата (2х2)  левого нижнего угла  8+3+5+1 = 17, оставшиеся же  числа дают совершенное  28 = 4 х 7 = 1+2+3+4+5+6+7 («треугольник» числа 7); суммы прочих трёх  малых квад­ратов - 19, 21 и 23. Некоторые из чисел  получают в «магическом квадрате» явное преимущество пе­ред другими: разности их по пери­метру (δ) образуются чередованием 1, 5 и 7 (Фиг.6.2. и 6.3.).

 

Возможно, что вы развлекались «магическим квадратом» когда-либо в детстве за партой во время скучного урока, а вот у Бенджамена Франклина, одного из основателей Соединённых Штатов, это увлечение сохранилось и в зрелые годы (видно, в его век трудно было занять себя ещё чем-либо стóящим, сидя битый рабочий день в офисе без ПК за столом). Каким образом почтенный Б.Франклин оказался упоминаем «в одной команде» с китайским оракулом и «загадкой НЛО», мы  расскажем немного погодя, пока же отметим уникальность и симметрическую простоту устройства числового квадрата 3х3.

Во-первых, это «взвешенное» расположение чисел девятки относи­тельно центра, представленного пятёркой (Фиг. 6.3.); причём любые девять  чисел, взятые подряд и расположенные по приведённой схеме в квадрате‚ дадут одинаковую сумму  при  сложении  по горизонталям, вертикалям и  диагоналям.

. 6.2.

При исключении  центра - числа 5 - сумма  в квадрате относительно «нулевого полюса» оказывается равной десяти:  то есть сумме священного тетракса пифагорейцев 1+2+3+4=10 и основанию десятичной  системы счисле­ния.

Две четверицы  - «прямая» и «обращённая» - составляют в сумме виналь (20),  который становится‚ таким образом‚ ни чем иным‚ как одним из представлений Октавы или восьми двоичных чисел Ба гуа (Фиг. 6.4). Не будет ошибкой утверждение, что эта обобщённая форма квадрата 3-х  заключает в себе  архетип декады - натуральной последовательности от единицы до десяти; и можно показать также её основополагающую роль для любых систем счисления, в каких бы мы ни оперировали[4].

Если  взять  девятку «от самого начала» - т.е.   от  нуля  в  соответствии с обозначениями восьми триграмм, где отсчёт открывается Кунь () или нулём двоичной системы, -  то суммой квадрата будет 12 (Фиг. 6.3а)‚  что указывает на Октаву теперь уже в «хро­матической» форме;  хотя её присутствие можно было предполагать из одного факта взвешенного распределения чисел  огдоады относи­тельно  центра.

 

                                                                                               

 

 

 

 

 

 

 

 

Проведём теперь деление единицы на 7. Выраженный в виде периодической десятич­ной  дроби результат имеет вид:

                   0,142857…     или   0,(142857) -

т.е. образует период  из шести цифр в данной последо­вательности,  исключая 3, 6  и 9.

1/7 - единственная дробь с числителем до десяти, обла­дающая  полным периодом:  максимальный период дроби m/n  (m и n - целые) не превышает значения числителя минус единица  (n-1). Легко  убедиться в том, что периоды рациональных дробей являются циклами или циклическими перестановками, в нашем случае  перестановкой  (142857):

1:7 = 0,(142857)

2:7 = 0,(285714)

3:7 = 0,(428571)

4:7 = 0,(571428)

5:7 = 0,(714285)

6:7 = 0,(857142).

 

 Период можно представить в виде графической диа­граммы, расписав цифры от 1 до 9 по кругу и соединив линией последовательно те из них, которые образуют цикл периода. В случае 1/7 подобным графом мы имеем  символ так назы­ваемой эннеаграммы Г.И.Гурджиева. Одна тройка из числа девяти (3, 6 и 9) не входит в период:  на эннеаграмме ею образован треугольник, обозначенный в круге пунктиром; а «прямая» и «обратная» ветви представлены двумя другими тройками  5, 8, 2   и  7, 1, 4 - (Фиг.  6.5).

Попытка связать эннеаграмму с ходом ступеней октавной гаммы известна нам также от Георгия Ивановича‚ -   правда‚ им ни разу не было использовано понятие квинты (хотя‚ конечно‚ музыку он знал отлично). В цикле эннеаграммы (142857) разности между соседними числами дают -3-2-6-3-2-6- в отношениях  3:2 и 2:1 - квинты и октавы.

         Из других трактовок эннеаграммы (а при­водимая нами здесь не известна  из школы Гурджиева) отметим следующую. Если  в Ло шу квадраты  3, 6 и 9 закрасить коричневым цветом, 5, 8 и 2 - оранжевым и 7, 1, 4 - голубым‚ то выделенные три тройки симметрично располагаются в «магическом квадрате»: 2-5-8 образуют диагональ, а 1-4-7 и 3-9-6 - два треугольника с вершинами соответственно в левом верхнем и правом нижнем углах - Фиг. 6.7.

            Из сравнения доктрин можно заключить - и засвидетельствовать в свою очередь  некоторыми демонстрациями -  что  триада 2-8-5 включает в себя «элементы развития»,   1-4-7 - «разделение целого», а 3-6-9 - его «уравновешивание». Нумерологические суммы троек (3+6+9 =18 =9, 2+5+8 =15 =6, 1+4+7 =12 =3) снова дают  нам 9, 6 и 3 с параллельным рядом значений:  9 - «карта мира», 6 - «октава» (6 квинт диатоники)‚ и  3 - «нераздельное и неслиянное» целое[5].

Пятнадцать  или  сумма квадрата по строкам, столбцам и диагоналям - всего восемь сумм - нумерологически составляет  шесть (1+5).

 

 

Используя паттерн квадрата согласно Фиг. 6.3. и свойства его симметрии‚ можно легко построить «бесконечную форму» 9 полей с сохранением   суммы  15 в квадратах 3х3 по строчкам и по столбцам - Фиг. 6.7 а. Размер 9 х 9  клеток имела доска  древнеиндийских шахмат - чатурранга‚ и фигуры на ней выстраивались с че­тырёх сторон;  позднее на её основе была разрабо­тана игра на поле 8 х 8 клеток‚ известная в настоящее время.  Квадрат 9х9=81   связывается с квадратом 8х8=64 через  семнадцать - третье про­стое число Ферма (Фиг. 4.55 а).

 

«Особенно предпочтительны для символического плана храма две мандалы: одна с 64 малыми квадратами‚  другая - с 81»‚ -

 

сообщает Титус Буркхардт[6]. 

Надо заметить‚ что повторяющимся элементом бесконечного паттерна 9-ти полей на плоскости будет не квадрат  9х9‚ как можно было бы предположить‚ а квадрат 12х12 (Фиг. 6.7а). Циклическая смена  числовых элементов проис­ходит в нём в соответствии с одним из двух ритмов: …-1-3-…  («шаг» равен 4)  или …-1-1-2-4-…(«шаг» равен 8). Суммы по диагоналям в составляющих квадратах 3х3 принимают здесь значения от 6 до 24 (Фиг. 6.7б.)‚  соотносящиеся как 1:2‚ 2:3‚ 3:4‚ 4:5 и 5:6 - октава‚ квинта и кварта‚ а также большая и малая терции (подобные же отношения мы нашли в геометрических элементах пяти платоновых тел - Фиг. 4.34).

 

Если цифры‚ входящие в период  эннеаграммы (142857)‚ распределить по две и полученные результаты поделить на 7, то мы получим  2-4-8  (14:7=2, 28:7=4, 57:7=8+1. Последняя 1 -  это та «лишняя» единица, что от­крывает следующий  нисходящий цикл; но далее подобная  процедура может быть продолжена уже делением на шесть: 24:6=4, 48:6=8. Последним делением на шесть мы имеем самую октаву:  48:6 =8.

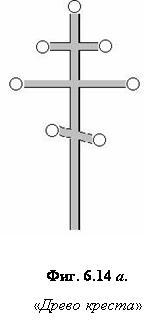Октава означает цикл, где первая ступень  совпадает с восьмой  (до = 1, до¹ = 8), а шесть промежуточных ступеней, делящих её на  интер­валы,  образуются квинтами в последовательности  фа-до-соль-ре-ля-ми-си (между си и фа нет интервала квинты) - или же, если брать ступени по по­рядку их расположения в октаве  (высотному возрастанию): 

 

                  

 

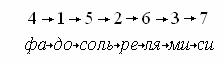
 Если принять фа, открывающую квинтовый круг, номером первым, то квинтовый порядок ступеней по их порождению (фа-до-соль-ре-ля-ми-си)  выражается в следующем виде:

                                                                                                                                                                                                                                                                                                                                                             

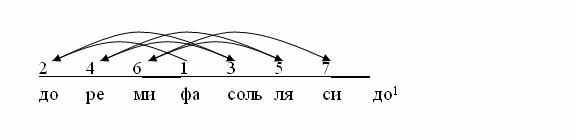
где слева от фа располагаются чётные, а справа – нечётные квинтовые номера.

Последовательность квинт может быть обращена от си к фа:  выше нами  показано, что ось двусторонней симметрии (диатоники) в круге  квинт проходит через фа и си, так что они представляют собой как бы «северный и  южный  полюсы» двенадцатиступенного круга Октавы.  Таким образом,  «4» и «7» переходят друг в друга, а  порядок ступеней можно изобразить таким образом:

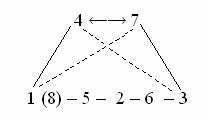
(где  до - это №№ 1 и 8) - Фиг. 6.8.

 

         Здесь мы снова обнаруживаем триады 1-4-7, 2-5-8 и 3-6-9. Девятая ступень, конечно, отсутствует в семиступенной гамме, но её отсутствие успешно восполняется полутоновыми интервалами  ми-фа (4-3) и си-до (1-7)‚  указывающими на необходимость  обратной, сим­метрической гаммы  си – соль^b – ре^b – ля^b – ми^b – си^b – фа, следующей по изменён­ным нотам и дающей полную картину «дерева жизни».

 Маятникоподобное раскачивание, подобное движению балансира часов‚ совершающее полные циклы дейст­вия и отмечающее «приход и возвращение» всего, что происходит в мире,  и  зафиксировано гурджиевским символом эннеа­граммы (Фиг. 6.5.). Деление  1:7 порождает шесть интервалов эннеаграммы аналогично  тому, как квинтовое деление в шесть ходов создает шесть тонов гаммы; при этом фа должна возвратиться в си, чтобы цикл не «разорвался» (Фиг. 6.9.). В древнегреческой теории музыки интервалы полутона‚ в которых «движение должно обратиться вспять»‚ так и назывались - лейммами («непроходимо­стями»).

 

Девятка или эннеада имеет соответствие с тоном.  3² – интервал це­лого тона,  основа деления в гамме семи ступеней; «накопление девяток» завершает семь ступеней диатоники в си интервалом тритон (фа-си) 3⁶ = 9х9х9, отмечающим диаметр  квинтового круга и определяющим  границы тональностей.

 

 

 

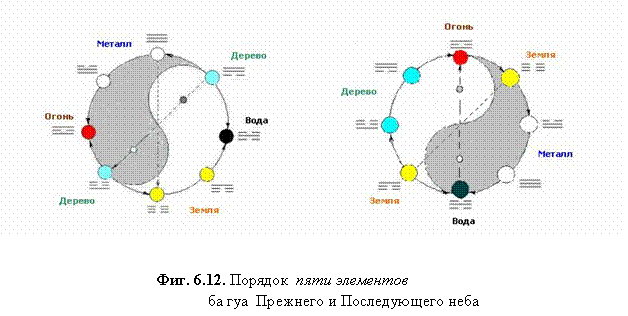
Рассмотрим расположение триграмм  Преж­него неба (Сянь тянь ба гуа) – универсального архетипа, одним из выражений которого также служит Октава (Фиг. 6.10.).

      

Начертания (гуа) триграмм и гексаграмм выражаются, строго говоря, не чи­словыми, но символическими значениями «инь» («женское») и «ян» («муж­ское»), и положение их в Прежнем небе определяется  «последовательностью порождения»:

 

 

 

         Ян при этом «опускается сверху», а инь «поднимается снизу», и три­граммы принимают двоичные значения от 0 до 7, если прочитывать их двоичные знаки (инь ─ ─ = 0,  ян  = 1) сверху вниз - как обычно и читают письмена иероглифов.

 Такая последовательность триграмм отражает порядок волнового движения, где нижний ряд черт (от которого традиционно ведётся счёт триграммы) отвечает волне с двумя полупериодами (2p),  то есть приме‚ второй ряд –  волне с четырьмя   полупериодами  (4p) или  первому обертону (октаве),  и верхний ряд –  волне с восемью полупериодами (8p) и третьему обертону (второй октаве). «Порядок порождения» следует также из   разложения бинома (а+ b)³, если принять а = (─ ─),  b =  (──) - см. Гл. 7.

 При таком  порядке  триграмм диаграмма Сянь тянь ба гуа (Прежнего неба) получает вид, представленный  Фиг.  6.10.

      Ход двоичных чисел  «порядка порождения» следует характерной S-образной кривой‚ «склеивающей» круг в точках 4-5 и 8-1‚  которая может быть сопоставлена «эллиптическому обращению»  гаммы относительно полюсов  фа и си. Здесь   снова выявляются симметричные триады 1-7-4 и 5-8-2, а  3 и 6  из «группы тройки» образуют горизонтальную ось: место девятки снова оказалось в «пустом цен­тре», через который осуществляется возвращение 8  в 1 и  4 в 5.

 

Видимо, существует нечто общее в строении октавы, «магического квадрата 3-х» и эннеа­граммы:  хотя  их генезис, казалось бы, различен,  в основе заключена сходная закономерность. Примечательно и то, что волновое движение и музыкальная гамма, по сути,  имеют отношение не к абстрактной математической, но к при­родно-физической сфере реальности.

       Легко заметить также (Фиг. 6.7.), что числа цен­тральной тройки эннеаграммы   3, 6 и 9 при де­лении на 3 имеют остатком 0 (т.е. равны нулю по модулю 3), правой  тройки  7, 1, 4 ─ единицу либо минус 2 (равны единице по модулю 3), а левой тройки  5, 8, 2 - минус единицу либо 2   (равны двум по модулю 3).

Симметрическое равновесие между этими модальными тройками отражено диаграммами  Ба гуа, если их триграммы увидеть, скажем, как трёхдольные размеры с акцентом на первой (),   второй  ()  или третьей () позициях.

 

«Смешанное» распределение триграмм Последующего неба (Фиг. 6.11.),  кажется, редко получает должное объяснение. Если сравнивать его с симметрией Прежнего неба, то оно на первый взгляд может показаться хаотическим, - но это только на первый взгляд (см. Гл. 7).

В Хоу тянь числа триграмм («порядка  порождения») образуют «крест» двух осей зеркальной антисимметрии, направлен­ных по «сторонам света»: 3-6  ()  - «север-юг» и 5-7 () ─ «восток-запад». Иньские и ян­ские черты при этом меняются местами, одновременно изменяя «направление». Пары 1-8 () и 2-4 () антисимметричны относительно горизонтальной оси (5-7), а самая пара 5-7 () - относительно вертикальной оси  (3-6).

В расположенных относительно центра поворотной симметрии парах 1-2  ()  и 8-4 () янский знак вступает сверху - опускается‚ иньский знак вступает снизу – поднимается‚ направления их движения противоположны.

Ниже мы рассмотрим роль подобных отношений в основе формирования семейств гексаграмм  Книги Пе­ремен - И  цзина.

 

Мы  останавливаемся на этих довольно сложных эволюциях триграмм  Последующего неба  по той причине, что видим в них идею непространственной симметрии - «нефёдоров­ской  кристаллографии» А.А.Любищева‚ проявлениями которой‚ по мысли последнего‚ могли бы служить морозные узоры на окнах‚ - а также  формы живых организмов[7].

 

Такая формообразующая система  являлась бы расширением известной группы пространственных симметрий Фёдо­рова-Шенфлиса -  описывающей  все возможные формы кристаллов. О прихот­ливой форме снежинок размышлял ещё такой проницательный математик и астро­ном‚ как Иоганн Кеплер, работы по «небесной механике» которого послужили, кстати, одним из отправных пунктов для  классических законов движения Ньютона. Возможно, что сходными  способами  по­лучаются цветные и странные симметрии семейств элементарных частиц  квантовой физики микромира.

 

Вкратце затронув вопросы строения «квадрата девяти полей» или «карты  мира», тут же отметим тождество её Древу Жизни кабалы или системе Сефирот - Божественных чисел - Фиг. 6.13.

В Древе Сефирот различаются правая (мужская), ле­вая (женская) и центральная (уравновешиваю­щая) колонки чисел-сфир; первая (Кетер - «Корона») и десятая (Малкут - «Царствие»)[8] аналогичны верхнему и нижнему пределам октавы, при этом верх­няя (Кетер) заключает в себе также «неразложи­мую триаду» - Айн Соф Аур [9].

 

читать дальше >>>

 

на главную