ааа

ОКТАВА

а КАКаа ФРАКТАЛЬНО-ЧИСЛОВОЙа ОБЪЕКТ

---------------------------------------------------------------------

Б. Сварог й

----------------------------------------------------------------------

 

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааа аа История квантовой эволюции была записана на языке чисел

в первыйа момент образования нашей вселенной

 

аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ааааа Тимоти ЛириВа История будущего

 

 

 

 

ааааааааа Октава является основным музыкальным термином и обозначает совпадение звуковВ частоты которых сонотносятся как 2:1. Вместе с тема октава есть лвосьмерица╗ (ὀκτώ - древнегреч.а лвосемь╗).

ааааааааа

ааааааааа Нетрудно понятьВ что основное свойнство консонанса двух звуков са отнношением частота 2:1 азаложеноа в принроде гармонической кривой:а в полном её периоде (2p) укладываются две полуфазы (p)В в двух полных периодах - четыре полуфазы и т.д.В что даёт при данном условии совпадение колебаний в фазовых точках:

 

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааа а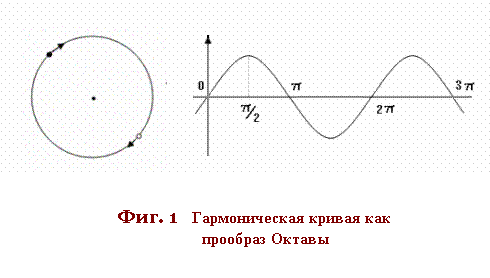

аааааааааааааааааа

ааааааааа Вместе с тем гармоническая кривая описывает простейший вид движения Ц осцилляциюВ а математиченски является элементарной периодической функцией:аа кривые других зависимостей могут быть разложеныа в суммыа бесконечного ряда гармоник.

 

ааааааааа Как же возникает в музыке разделенние интервала максимального консоннансаа 2 - октавы - на промежуточнные интервалы? Ответ на этот вопрос содернжится в древнейшей из известных истории систем музыкального строя - квинтовойВ названной по имени Пифагора. Исторически так повелосьВ что корни всего могут быть найдены в ГрецииВ однако же нет оснований полагатьВ что этот принцип не был извеснтен куда ранее в ЕгиптеВ ВавилонеВ Инндии и Китае.

 

ааааааааа Колебания струны порождают частичные тоны (обертоны)Ва соотносящиеся как целые числа 1:2:3:4:5... Квинтовое деление основано на втором обертоне и слендующем за октавой консонансеа -а отношении частота 3:2.а Как доказываета опыт со струнами различной длиныВ чем проще в числовом выраженнии отношение их длинВ тема приятнее сочетание колебаний на слух и полнее синнергия (явление резонанса) между ними.

а

ааааааааа Назовём октавный интервал адо-до¹. СтупеньВ относящаяся к тонике до по частоте как 3:2 нанзывается квинтой и традиционно обознанчаетсяа соль. Из определения интервала октавы следуетВ что отношение верхннегоа до¹ к соль составит при этом 4:3В и это гармоническое отношение известно как кварта или обращённая квинта. Если заставить звучать три струныВ настроеннные ва доВ соль иа до¹ одновременноВа в аккорде будут присутствовать сразу три интервала - октава 2:1 В квинта 3:2а иа кварта 4:3. Древние зналиВ чтоа квинта и кварта взаимообратимы - то есть симнметричны в отношенииа октавыВ и если соль есть квинта к доВ то фа - квинта к до¹В иа обратно -а фаа по отношению к до составляета квартуВ а соль - кварту к до¹.

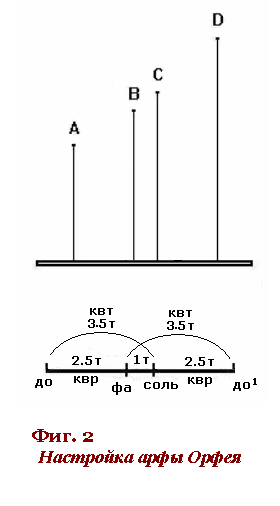
ааааааааа Эту пропорциюа можно представить в виде

 

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааа до: фа: соль: до¹ = 1: 4/3 : 3/2 : 2В

 

и она определяета первый гармонический паттерн октавы - так назынваемую нанстройкуа орфеевойа арфы. Данное вынражение содернжит в себе всеа известные в древности отношения - а именноа арифнметическую, геометринческую и гармонинческую пропорции, а также принцип зонлотого деления. Два его средниха члена при этом сонотнонсятся кака 9:8В то есть обранзуюта интервала натурального целого тона - Фиг. 2. Таким образомВа нанстройка арфы Орфея содержит алгоритма (гномон)В посредствома которого на оснонвании отношеннияа первых четырёх членов натурального ряда (греч. τετραξ - четвенрица)а могут быть установлены всеа мунзыкальные стунпени.

 

ааааааааа Как это возможно? Последующее построениеа есть хорошо знакомыйа мунзыкантама лквинтовый круг╗. Чтобы квинта первой четвёркиа в свою оченредьа образовала октавуВ достаточно изменить длину соответствующей струны вдвое.а Кварта в октавеа соль-соль¹ по-прежнемуа до¹ В а квинтойа станновится ступень ре¹:

аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа 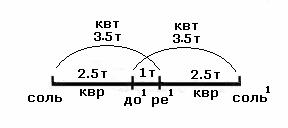ааааааааа ааааааааа ааааааааа аЕсли для удобства мы примем за исходную ступень в октаве до - до¹ фа со значеннием 1В тоа квинту от афаааа до¹ = 1 х 3/2 =а 3/2аа мы должныа понизитьа вдвоеВ чтобы она пришлась в одну октаву с фаВ совпав с тоникой до:

 

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа до = 3/2 : 2 = 3/4.

 

ааааааааа Тогда соль определяется как вторая квинта от значения до = 3/4:

а

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа соль = 3/4 х 3/2 = 9/8.

ДалееВаа ре¹ являетсяа квинтой от соль:

 

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ре¹а = 9/8 х 3/2 = 27/16В

 

иа величинаа 27/16а также должна быть уменьшена вдвоеВ поскольку вновь полученная ступеньа превысила верхнюю границу октавы до¹:

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ааааааааааааааааааааааааааааааааааааа аре = 27/16 : 2 = 27/32.

ааааааааа Между до и ре - также как между фа и соль Ц лежит интервал целого тона:

27/32 : 3/4 = 9/8.

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ааааааааа а

ааааааааа Четвёртая по счёту квинта строится от ступени реа 27/32а х 3/2= 81/64,а и носит названиеа ляВ приходясь в ту же октаву. ааа

ааааааааа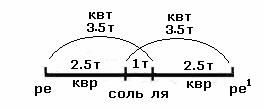

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа а

ааааааааааааааааааааааааааааааааааааа а

ааааааааа Между ля иа сольа интервал целого тона:аа 81/64 : 9/8 = 9/8.ааааааааааааааааааааааааааа ааааааааа

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа

 

ааааааааа Пятая по счёту квинта (ми) строится от ля:а 81/64 х 3/2 = 243/128В

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа а

иа должна быть приведена в одну октаву с ней:

аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ми = 243/128 : 2 = 243/256.

аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа

ааааааааа 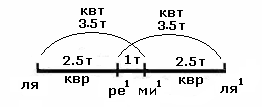ааааааааа

ааааааааа Ми образует целотоновый пронмежуток с ре:аа 243/256 : 27/32 = 9/8.

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа

 

ааааааааа Шестая по счёту квинтаВ которая строится от ноты ми и лежит в одной с ней октавеВ называется си:

аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа си = 243/256 х 3/2 = 729/512.

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа а

 

аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа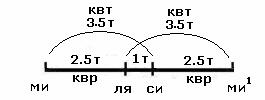

аМежду аля и си такжеа интервал целого тонаа 729/512а : 81/64а = 9/8.

 

аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа а

 

 

аааааааааааааааааа

Мы видимВ как квинтовый алгоритм действует совершенно автоматически и единообразно. Сведёма вменсте полученнные резульнтаты:

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ааааааааааааааааааааааааааааааааааааа

ааааааааааааааааааааааааааааааааааааа ааааааааа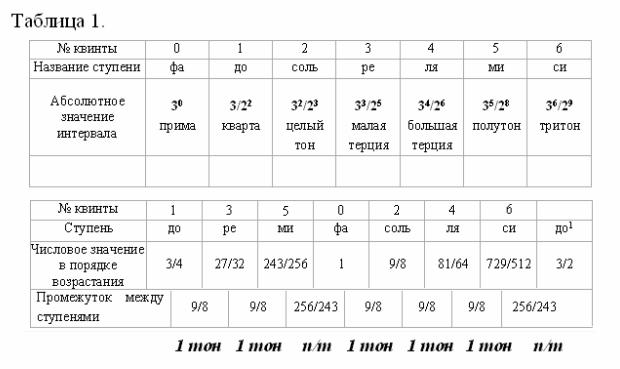

 

Две последние ступениа ми и си образовали новые интервалы внутри октавы:

 

аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа а Отношенияааа фа / миааа 1: 243/256 = 256/243

аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ааа иаааааа до¹ / сиаа 3/4: 729/512а = 256/243,

 

соответствуюта интервалу лейммыВ называемой иначе полутоном.

 

ааааааааа аЛеймма по-гречески лнепроходинмость╗Ва иа означает прекращенние заполнения октавного промежутка интервалами в 1 тон. В самом делеВ интервал 2 (октава) может вместить только 5 интернвалов 9/8а и 2 интервала 256/243:

 

ааааааааааааааааааааааааааааааааааааааааааааааа (9/8)⁵ х (256/243)² = 2.

 

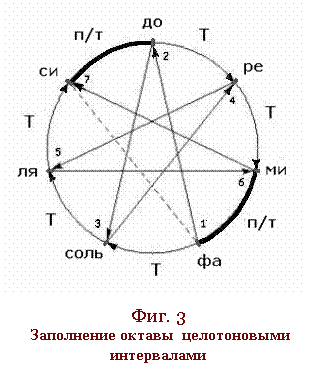
ааааааааа Такое естественное заполнение октавного промежутка (2) тоновыми интерваламиа с образонваннием семиступенной понследовательности

 

ааааааааааааааааааааааааааааааааааааа тон-тон-п/т-тон-тон-тон-п/т а

 

называется адиатонической (мажорнной) гаммой основных музыкальных ступеней.

а

Шесть интервалов (3¹-3⁶) Таблицы 1В полученные 1-6 квинтами (а также обращенияВ дополняющие иха до октавы) содержат основу для всех музыкальных построений. Обращённая же прима (3⁰) соответствует самой октаве (2).

Продолжение квинтового алгоритма заставита новые ступени лвклининваться╗ в тоновые промежутки менжду основными ступеннями:

аааааааааааааааааааааааааааааа VII квинта есть 3⁶/2⁹ х 3/2 = 3⁷/2¹⁰, поскольку же она прихондится на вышележащую октаву (превышая значение до¹=3/2), это числоа должно быть разделёно на 2,а что даёт 3⁷/2¹¹;

аааааааааааааааааааааааааааааа VIII квинта 3⁷/2¹¹х3/2=3⁸/2¹² >3/2,

апоэтому 3⁸/2¹²:2=3⁸/2¹³;

аааааааааааааааааааааааааааааа IX квинта 3⁸/2¹³х3/2=3⁹/2¹⁴;

аааааааааааааааааааааааааааааа X квинтааа 3⁹/2¹⁴х3/2=3¹⁰/2¹⁵>3/2,

ааааааааааааааааааааааааааааааааааааааааааааааааа апоэтому 3¹⁰/2¹⁵:2=3¹⁰/2¹⁶;

аааааааааааааааааааааааааааааа XI квинта 3¹⁰/2¹⁶х3/2=3¹¹/2¹⁷;

аааааааааааааааааааааааааааааа XII квинтаааааааааа 3¹¹/2¹⁷х3/2=3¹²/2¹⁸>3/2,

ааааааааааааааааааааааааааааааааааааааааааааааааа поэтому 3¹²/2¹⁸:2=3¹²/2¹⁹.

 

ааааааааа Все последующие ступени после первых семи (образованных с 0 по 6 квинту) обозначаются как изменённые (повышенные либо пониженнные) основнные ступени. Седьмая квинтовая ступень ниже на полутон (2⁸/3⁵)а ступениа соль: 3²/2³ : 2⁸/3⁵ =3⁷/2¹¹, поэтому онаа называется соль-бемоль (соль^b). Восьмая квинта есть пониженная на полнтона ре, так как 3³/2⁵:2⁸/3⁵=3⁸/2¹³В и соотнветствует ре^b. Девятая, точно также Ц ля^b (3⁴/2⁶:2⁸/3⁵=3⁹/2¹⁴), десятая Ц ми^b (3⁵/2⁸:2⁸/3⁵=3¹⁰/2¹⁶), одиннадцатая Ц си^b (3⁶/2⁹:2⁸/3⁵=3¹¹/2¹⁷). Наконец, двенадцатая квинта приходится на понниженный на полтона интервал седьмой, понскольку 3⁷/2¹¹ (соль^b) : 2⁸/3⁵=3¹²/2¹⁹. Слендуя принятому обозначениюВ мы должны отметить эту ступень как сольВ дважды пониженную наа полтонаа (соль^bb).

 

ааааааааа В пифагорейском натуральнном строе два полутонаа (дубль-бемоль) не дают в сумме интернвала, равного целому тону (2⁸/3⁵х2⁸/3⁵=2¹⁶/3¹⁰ <9/8)В поэтому последняя ступень не совпадает с фа №1 - не равна в точнонсти единицеВ то естьа иннтервалу примы,а превышая её на велинчину пифагорейской коммы:

 

3¹²/2¹⁹=531441/524288 =1.0136432 >1В обозначаенмой нами D.

 

ааааааааа СледовательноВ двенадцатая квинта вверх от исходной стунпениа порожндает новыйа малый интервала 3¹²/2¹⁹ в фа № 13 (Фиг. 5)В чиснленно равный разнице целого тона (9/8) с двумя полунтонамиа 3²/2³ : (2⁸/3⁵)² = 3¹²/2¹⁹, что составляет принмерноа 1/8,69а целого тона (иначе говоря, 1.0136432^8,69 = 9/8). Образование микроинтервалов (лкомм╗) в квинтовом строе задаёт числовую основу системы натуральной микрохроматики (см. 53-ступенная музыкальная система). Полное заполнение интервала октавы полутоновыми ступенями даёт естественную (12-ти или 17-ти ступенную) хроматическую гамму. При этом восходящие квинты (по часовой стрелке круга) образуют ступени бемоля ()В а нисходящие 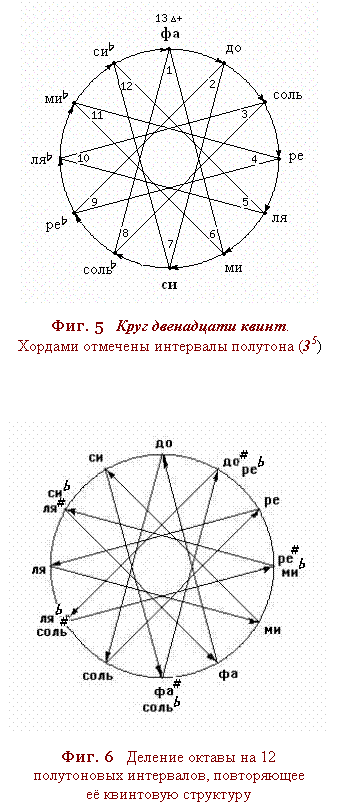(против часовой стрелки) - ступени диеза (#) - Фиг. 6В 7а [1]

 

ааааааааа ОчевидноВ чтоа на этом квинтовому процессуа не положен прендел. Если продолнжать его данлееВа все ступени квинтами вверх будут повторяться с повышеннием на комму (+D) с каждым виткома спиралиВ иа при движении квинтами вниз (последовантельнные значения умножаются на 2/3В и также приводятся в исходную октаву) -а с убынванием (−D) в каждом цикле двенадцати.а Мы предоставляем проверить это самому читантелю.а

 

аДеление отрезкаа до - до¹ гармоническими числами посредством итераций

 

ааааааааааааааааааааааааааааааааааааааааааааааа

 

(сравните с известным Преобразованием пекаря) бесконечноВ и при этома никогда не происходит совпадения положенияа двух различных номеров по той простой причине, что все ступени выражаются через степени чисела 2 и 3, являющихся взаимно простыми.аа

 

 

 

 

ааааааааа

 

Отметим основные моментыВ инванриантные относительно знанчений ступенейВ полученныха квинтовым алгоритмом - достанточноВ чтобы их номера шли по порядку [2]:

 

1.а каждые 12 последовательнных ступенейа образуют натунральную хронматическую гамму с подразделением октавы на 12 полутонов- Фиг. 6;

 

 

2. 17 последовательно взятых ступеней образуют семнадцатинступенную хроматическую гамму 12-ти полутонов с энгармонически неравными повышенными и понинженными ступенямиВ разделённнымиа интерваламиа коммы (D) - Фиг. 7;

 

а3.а каждая тринадцатая ступень замыкает октавный циклВ порожндаяа сдвиг на микротоновый интернвал (комму D) - Фиг. 5;

 

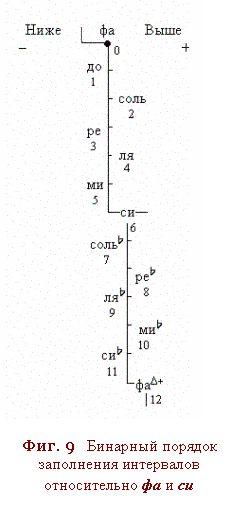
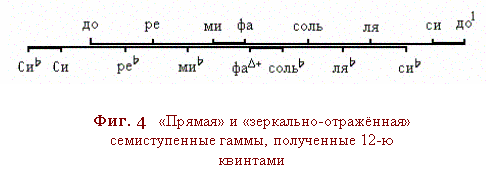
4.а каждый диаметрВ проведённый череза противолежащие ступениа двенадцатичленного кругаВ отменчаета в нём ось зеркальной симметрииа иа дваа полюсаВ относинтельно которых проявлен двоичный паттерн Октавы - Фиг. 4В9;

 

5.а каждые 7 следующих по порядку ступенейВ отделённых диаметром (Фиг. 10) образуют семиступенную гамму с пятью целотонновымиа и двумя полутоновыми пронмежутками одного из семи принятых в античнонсти ладов (либо заменяющей лад тональности) а- сенмеричныйа паттерн Октавы:

ааааааааааааааааааааааа

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа аааа

 

аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа

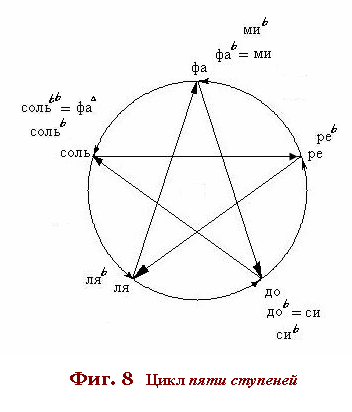
6.а все вышеуказанные свойнстваа Октавы определены еёа пянтеричныма циклом:аа пятьа квинт вверх результируют поннижением исходной ступени на полнтонаВа либо повышением на полтона при движении квинтами вниз - Фиг. 5В 8;

 

7.а далееВ двенадцатеричный поряндока разбивается на лквадранты╗ и лтригоны╗а малой и больншой терцийВ служащих в музыке основойа аккордово-гармонических построений - Фиг. 11;

 

8.а иВ наконецВ все описанныеа отнношения проистекают из начал чёта и нечетаа (3ⁿ : 2^m)В заложенных в квинтовый алгоритм.а Свойства Октавы как умозрительного объектаа не зависят от природы звукаВ и вправеа рассматриватьсяа кака проявление законов числа. Сходные принципы числовой организации обнаруживаются и в ДНК Ц универсальном коде жизни.

а

ааааааааа Присутствие коммы в квинтовома круге было известно издавна и служило постоянным раздражающим фактором для музыкальных теорентиков. Им казалосьа неудобным образование в натуральном строе тональных гамм с комматически смещённными ступенямиВ а также и тоВ что октава не замкнута - два натуральных полутона не образуют в точностиа целый тон. Уже греческий философ АристоксенВ ученика Аристотеля (IV в. до н.э.) предложила темперированныйа строй -а деление октавы на равные интервалы. Но эта рационалистическая идея смогла осуществиться лишь во второй половине XVII векаВ когда каждый полутон объявили равным ровно 100 центамВ или .

ааааааааа

ааааааааааааааааааааааааааааааааааааааааааааааа

ааааааааа

аааааааааааааааааа ааааааааа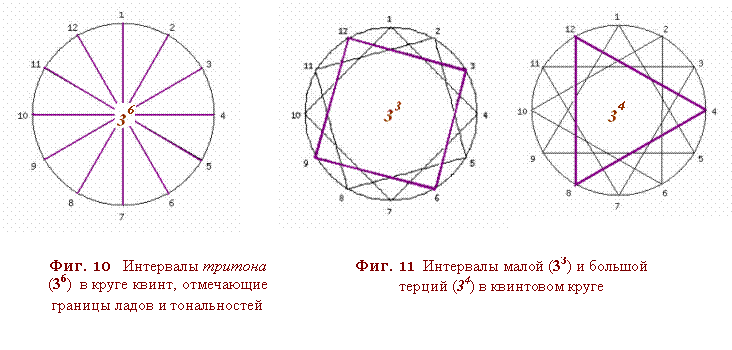

 

Это дало возможнностьВ бесконечно поднимаясь по лестнице квинтВ неизменно возвращаться к её началу -а как мы видим на знаменитой гравюреа Маурица Эшера,а и в чёма убеждают нас органные произведенияа Иоганна-Себастьяна Баха.

ааааааааа Ноа теВ кто стоял ближе к основаниям квинтовой системыВ не могли не сознавать её фрактальные возможнности -а об этом свидетельствуют известные места платонова Тимея (36).

 

ааааааааа Продолжим итерации виток за витком двенадцатиступенного круга. Нетрудно убедитьсяВ что на пятом круге будет достигнуто приращение в 4 коммыВ что превышает интервал полутона (3.85 D). Тогда ступеньа 12х4+6 = №54а ми станет на полтона вышеВ то есть лобратится╗ ва фаВ а лквинтовая спираль╗ пересечёт самое себя во второй раз - первое сближение мы видели в №13. На сей разВ показывает расчётВ лсоединение╗ будет более полным Ц новый микроинтервал (s) в 6.5 раз меньше пифагорейской коммы (D)В аа лвитки спирали╗ стали знанчительно шире.

 

ааааааааа Отправляясь от нового значенияВ мы вправе ожидатьВ что на седьмом круге цикла в 53 квинты s-приращенния достигнут величины DВ и снова произойдёт лсоединение╗ с единичным фа. При этома ступень №54 + 53 х 6 = 372 достигнета (и превысит ещё на какое-то микротональное деление) величину стунпени №13 фа^D. Если №13 приходит в соответствие с № 372В то №1В очевидноВ отвечает а372─12 = № 360В так что следующее лвозвращенние╗а происходит ровно на этом номереВ что подтверждается компьютерным моделированием пифагорейских гармонических чисел Ц Фиг. 12.

 

ааааааааа Не боясь наскучить читателюВ мы не откажем себе в удовольствии провести расчёт лна пальцах╗ и следуюнщего соединения. Поскольку интервал окнтавы 2 содержит 51 микротон I порядка D плюс один микнротон II порядка sВ то приращение комм D с каждым циклом 12-ти ступеней за 51х12=612 номенров покроет интервал в 51DВ а для получения малого приращения sВ как мы знаемВ нужен ещё период в 53 ступени. Прибанвив к №1фа 51 цикл по 12 нонмеров и один в 53 номераВ мыа получим искомое значение ступени а№1+612+53 = №666 - самое близкое после единицы среди более чем 16000 гармонических чисел (этот микроинтервала составнляет 1/15878а часть октавы) - Фиг. 12. ТакВ занимаясьа вродеа вполне безобидным деломВа мыа невзначайа затронулиа лэсхатологическую╗ тему.

 

ааааааааа 54а в действительности есть сумма лдвойных иа тройных чисел╗В приводимых в Тимее в качестве основы расчлененияа Октавыа космоса:

 

аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа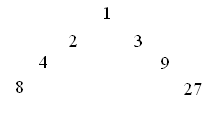

 

 

ааааааааа 360 атожеа хорошо известно -а до сих пор так считают градусы окружностиВ но причём здесь лчисло Антихриста╗? Ответ может заключаться в томВ что 666 не менее других паттернов Октавы пригодно для представления временных цикловВ ведь

 

лустрояяа небо, Она творит... вечныйа образ, движунщийся от числа к числу,а которыйа мыа назвалиа временем╗

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа (ТимейВ 36b).

 

ааааааааа Время - лматерия╗ столь же привычная для насВ сколь и непонятная - по свидетельству всех мистиковВ есть принцип фрактального раздробления Единого Бытия.

 

ааааааааа Каждый иза периодов Октавы отвечает гамме с соответствующим микротональным делениемВ поддержинвая основное фрактальное свойство - создавать циклы внутри цикловВ повторяя одни и те жеа числовые узоры в нисходящем порядке шкалы масштабовВ -а возьмём известное множество Мандельбро.а В этом смысле мы можем говорить о лвнутренних октавах╗ [3] В вкладываемых друг в друга наподобие матрёшек. Период в 665 квинт выступает при этом характерным аттракторомВ повторяющима в своём интервале исходный рисунок двенандцати стунпеней - аФиг. 13:

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа

ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ааааааааааааааааааааааааааааааааааааааааааааааа

ааааааааааааааааааааааааааааааааааааааааааааааа ааааааааа 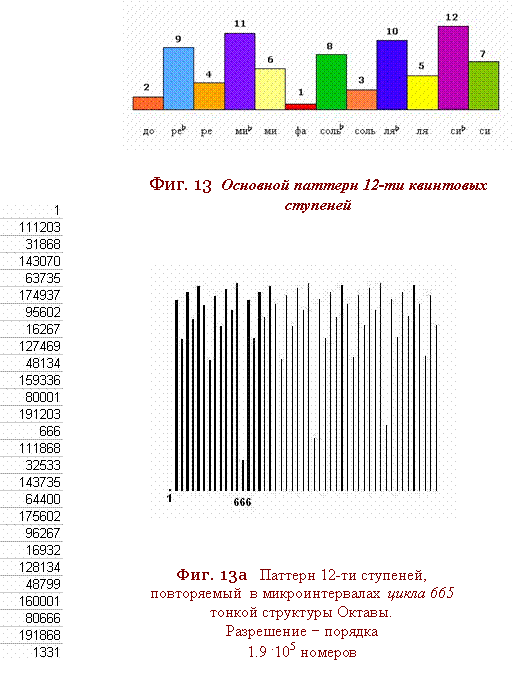аааааааааааааааааааааааааааааа аааааааааааааааааааааааааааа аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа

 

Периоды более высоких порядков раскладываются на нижележащие как на составляющие модулиВ свянзующима звенома выступаета цикл 665:

а

аааааааааааааааааааааааааааа 16266ааа =ааа 665аа ха 24а +а 359 ─ 53В

аааааааааааааааааааааааааааа 31867ааа =а 16266а хаа 2а ─аа 665В

аааааааааааааааааааааааааааа 79335ааа =а 16266а хаа 5а ─а 665а ха 3В

аааааааааааааааааааааааааааа 111202а =а 16266а хаа 7а ─а 665а ха 4В

аааааааааааааааааааааааааааа 190537а =а 16266а ха 12 ─а 665а хаа 7Ва

аааааааааааааааааааааааааааа 301739а =а 16266а ха 19 ─а 665а ха 11Ва и т.д.

 

 

В концеа XVI векаа француз Жозеф Скалигер задумал создать времяисчислениеВ наилучшим образом сонгласованное с известными на то время астрономическими и историческими даннымиВ иа предложил так назынваемый юлианский период в 7980 летВа попав как раз лв яблочко╗В поскольку эра Скалигера - до сих порВ кстатиВ используемая при хронологических расчётахВ -а основана как раз наа периоде 665:

 

7980 = 665 х 12.

 

а Вряд ли СкалигерВ да и Святой Иоанн опирались наа непосредственное знание об ОктавеВ но её следы уводят гораздо глубже. Носящая имя Пифагора квинтовая система по своей математической простоте и универсальности является бессмертным памятником - а также и универсальным кодом человечества: если даже предположитьВ что знание о ней было бы когда-либо утраченоВ она неизбежно была бы переоткрыта заново. Странные лмистические╗ принципыВ положенные древними в основания природы и применяемые в астролонгии и счёте времени - пара инь-янВ три гуныВ пять элементовВ восемь направлений и двенадцать знаков ЗодиакаВ загадочный И цзинВ китайский шестидесятилетний циклВ майанский календарь и древнеиндийские эры - все они так или иначе находят в Октаве свой числовой прообраз.

 

 

а

Словарь музыкальных терминов

 

на главную