ЗВУКИ
ПРЕВРАЩЕНИЙ
ДИКОЙ СЛИВЫ
МЭЙ
ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа
Б.СВАРОГ╙
Молодой
Дракон
пустился в
путь от
Западной
Страны и
достиг
севера горы Юаньюй.
Нашёл
растущий в
лощине Сеси
бамбук,
выбрал часть,
ровную по
всей длине, вырезал
посередине
между
коленцамиЕ Затем
сделал
двенадцать
таких
трубочек, а когда
услышал
пение пары
фениксов у
подножия
горы Юаньюй,
понял, как
должны
разделиться
двенадцать люй: шесть
должны быть
подобны
голосу самца,
а шесть Ц
самки
(Люйши чуньцюВ 5В6)
Приложенияа И
цзинаа
ва
астрологическиха прогнозаха
поднимаюта вопрос
о связи его с
календарёмВа а
такжеа
с десятью и
двенадцатью
знаками
шестидесятеричного
циклаа
иа
квинтовой музыкальной
системой. Эти
аспекты И цзина
были вполне
разработаныВ
по-видимомуВ
по нашим
меркам
довольно
давно Ч ещё в
до-ханьскую
эпоху. Об
этом
свидетельствуетВ
в частностиВ
известная
практика
соотнесения
пяти первоэлементова иа
двенадцати циклических
знаков со
ступенями
звукорядаВ
называемая
лвведением
звуков╗ (на инь).а
Существование
соответствующих
астрологических
расчётов и
гаданий
вовсе не
означаетВ
однакоВ что
принципы
такого соотнесения
достаточно
ясны и
очевидны. При
этом
невозможно
оставить в
стороне и
тему более
общую Ч о
характере
системы 64-х
гексаграмм
вообще. Секрет
их
лправильной╗
аранжировки,
возможно,а
содержит не
что иное, как волну
времени Ч
ключ к
организации
временных
событий.
аааааааа Мы
исходим здесь
из того
здравого
предположения,
что секреты Книги
Перемен
заключены в
её
собственных
свойствах. Оставаясь
в рамках
общего
подходаВ мы
не претендуем
на полноту и
исчерпанность
рассмотрения.
Многие
востоковеды
на основе китайских
источников
упоминали о
связи циклических
знаков
шестидесятеричного
цикла с
системой
музыкальных
тонов.
Допущение
это отнюдь не
безосновательноВ
если в
качестве
основы брать
квинтовую
систему. 5 и 12
составляют в
ней основные
циклы: на
каждые пять
квинт
приходится
понижение
высоты исходной
ступени на
полтонаВ а на
каждые двенадцать
квинт Ч
повышение её
на микротон
Δ (так
называемую
лпифагорейскую комму╗). а
 Таким образом, за
двенадцать
циклов пяти квинт
мы
проходим
полутоновыми
шагами весь
промежуток
октавы
(двенадцать
полутонов)В а
исходная
ступеньВ в
свою очередьВ
приобретает
дополнительное
приращение 5DВ Ч
всё это было
подробно
рассмотрено
нами в другом
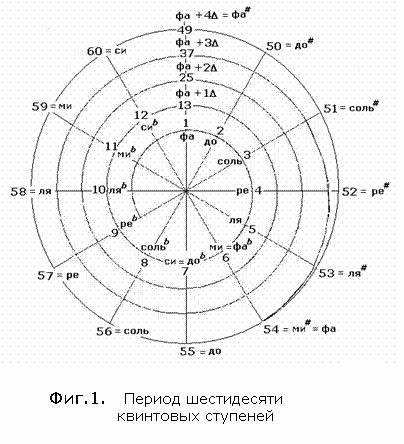
месте (Октава). Важно
заметитьВ что
в этом
квинтовом
цикле порождается
микротоновая
гаммаВ в которой
№60 отвечает си ,
а №64 Ч миb в октаве
53-х ступеней - Фиг.
1.
Таким образом, за
двенадцать
циклов пяти квинт
мы
проходим
полутоновыми
шагами весь
промежуток
октавы
(двенадцать
полутонов)В а
исходная
ступеньВ в
свою очередьВ
приобретает
дополнительное
приращение 5DВ Ч
всё это было
подробно
рассмотрено
нами в другом
месте (Октава). Важно
заметитьВ что
в этом
квинтовом
цикле порождается
микротоновая
гаммаВ в которой
№60 отвечает си ,
а №64 Ч миb в октаве
53-х ступеней - Фиг.
1.
Построение
системы
квинтовых тонов-люйВ а
также их
связь с правильными
ветрами
(пятью
элементами и
восемью
триграммами)
и световым
циклом
приводится в Люйши чуньцюВ
сочинении III века до
н.э. [1]:
лКогда
состояние
мира харакнтеризуется
высокой
мудростью и
предельным
следованием
закону ли, ци неба и
земли,
совокупляясь,
понрождают звучащие
ветры.
Солнце,
двигаясь в
зодиакальной
плоскости от
одной точки
солнцестояния
к другой,
каждый месяц
образует с
луной
систему
наподобие
колокола,
порождая один
за другим
двенадцать
тонов люй.
Во вторую
луну зимы, в
день
солнцестояния,
рождается хуанчжун,
в последнюю
луну зимы Ц далюй.
В первую
весеннюю
луну Ц тайцоу,
во вторую Ц цзячжун,
в
последнюю Ц гусянь. В
первую
летнюю луну Ц чжулюй,
во втонрую, в
день
солнцестояния
Ц жуйбинь,
в
последнюю Ц линьчжун.
В первую
луну осени Ц ицзе, во
вторую Ц наньлюй,
в третью Ц уи.
В первую луну
зимы Ц инчжун.
Если ветры-цы,
создаваемые
ненбом и
землёйВ
правильны,
двенадцать
тонов верны╗ .
Последовательность
месяцев светового
года от
одного
зимнего
солнцеворота
к другомуВ
фазы
нарастания и
убывания луны
в каждом месяцеВ
равно как
и лдвухчасия╗ дня
и ночи
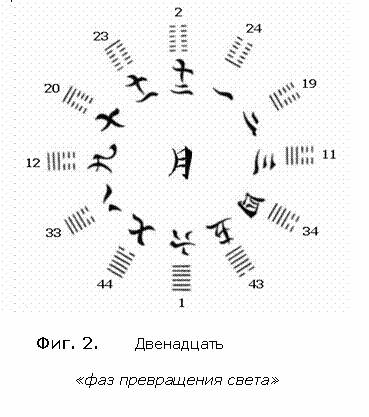
традиционно описываются
кругом
двенадцати гексаграмм
лпревращения
света╗ би гуаВ в
которых с
каждой
стадией
прибавляется
или убывает
одна сильная
черта ян - Фиг.
2. В свою
очередь это
позволяет
каждому промежутку
времени
сопоставлять
один из двенадцати
(а также и
десяти)
циклических
знаков. Шесть
оппозитных
пар би
гуа
располагаются
по диаметрам
кругаВ при
этом их
свойства
реверсивности и
оппозитности
определяются
относительно
двух перпендикулярных
осей 1-2а
и 11-12.
Гексаграммы
лпревращения
света╗ Ч будем
назовать их
лкардинальными╗
Ч задают
первый
двенадцатеричный
циклВ и мы
вправе
принять его
за основу для
распределения
всех
остальных
гексаграмм
согласно с
квинтовой
системой Фиг. 1.
В круге
двенадцати
ступеней
квинтовый и хроматический
порядки (по
полутонам)
обладают
взаимнооднозначным
соответствием
и обратимы,
тогда как
звуки, следуя
Люйши
чуньцю,
строятся
квинтами
вниз (т.е., в
западной нотации,
от си).
Как
известноВ в Чжоу и
лКниги
Перемен╗
(лпоследовательности
Вэнь-вана╗) гексаграммы
располагаются
по
реверсивным
либо оппозитным
парам (в
последнем
случаеВ когда
переворачивание
не изменяет
гуа). Можно
также
показатьВ
что
гексаграммы
группируются
в естественные восьмёрки в
соответствии
со своими
основными
свойствами
симметрииВ а
также
образуют
иные группы.
Обратим вниманиеВ
что пары 1-2 и 11-12
отвечают
наиболее
простому
симметрическому
отношению: их
нижняя и
верхняя
триграммы
либо
совпадают (А)В
либо
оппозитны (О).
Такой
тип
симметрической
связи
прослеживается
в первых
двух
восьмёрках
гексаграмм:
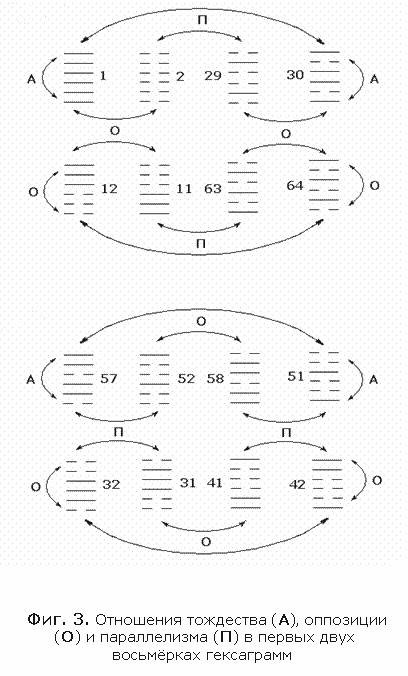
 В этой группе
шестнадцати
представлены
все лчистые
знаки╗ - т.е.
восемь
гексаграммВ
образованных
удвоением
нижней
триграммы: 1-2В 29-30В 51-57 и 52-58.
Пары 1-2 и 11-12
ранее
отнесены
нами к
лкардинальным
знакам╗. В
шести других -
реверсивно
несимметричных
-
гексаграммах
появляется дополнительное
новое
качество
симметрии:
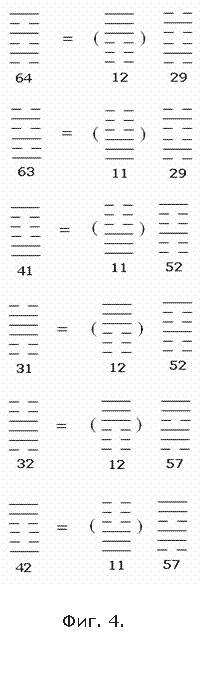
они могут
быть получены
путём
лумножения╗ адвух
кардинальных
11 и 12 на
лчистые
знаки╗ 29В 52 и 57 (Фиг.
4). При
лумножении╗
двух черт,
находящихся
на одной
позиции,
сильная
черта меняет
значение
другой на
противоположное,
слабая же оставляет
его без
изменения.
Этой
операцией вводится
алгебра на
множестве гуа И
цзина Ч что
было, кстати,
неявно
использовано
уже Цзин
Фаном (подробнее
см. )
В этой группе
шестнадцати
представлены
все лчистые
знаки╗ - т.е.
восемь
гексаграммВ
образованных
удвоением
нижней
триграммы: 1-2В 29-30В 51-57 и 52-58.
Пары 1-2 и 11-12
ранее
отнесены
нами к
лкардинальным
знакам╗. В
шести других -
реверсивно
несимметричных
-
гексаграммах
появляется дополнительное
новое
качество
симметрии:
они могут
быть получены
путём
лумножения╗ адвух
кардинальных
11 и 12 на
лчистые
знаки╗ 29В 52 и 57 (Фиг.
4). При
лумножении╗
двух черт,
находящихся
на одной
позиции,
сильная
черта меняет
значение
другой на
противоположное,
слабая же оставляет
его без
изменения.
Этой
операцией вводится
алгебра на
множестве гуа И
цзина Ч что
было, кстати,
неявно
использовано
уже Цзин
Фаном (подробнее
см. )
Располагающиеся
по диаметрам
окружности Фиг.
2 лкардинальные╗
гексаграммы взаимно
оппозитныВ и
можно легко убедитьсяВ
что при
лумножении╗
этих
двенадцати
на три чистые
знака 52В 29 и 57,а
которые мы
назовёма
модифицирующими
(а эти
последние
есть также
лшаблоны╗
основных
симметрических
отношений
лпараллелизма╗
П, лоппозиции╗
Оа иа
лкоординации╗
К1 и К2),а могут
быть
получены
новые 18 пар
гексаграмм
второгоВ
третьего и
четвёртого
циклов 12-ти (Фиг.
5):
ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа аааааааааааааааааааааааааааа 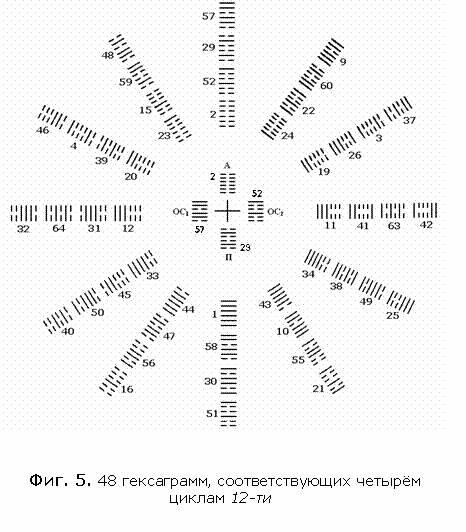
ааааааааааааааааааааааааааааааааааааааа
Полученные
последней
процедурой
гексаграммы
по свойствам
внутренней
симметрии
группируются
в четыре
новые
восьмёркиВ
дополнительно
к уже
имеющимся
двум:
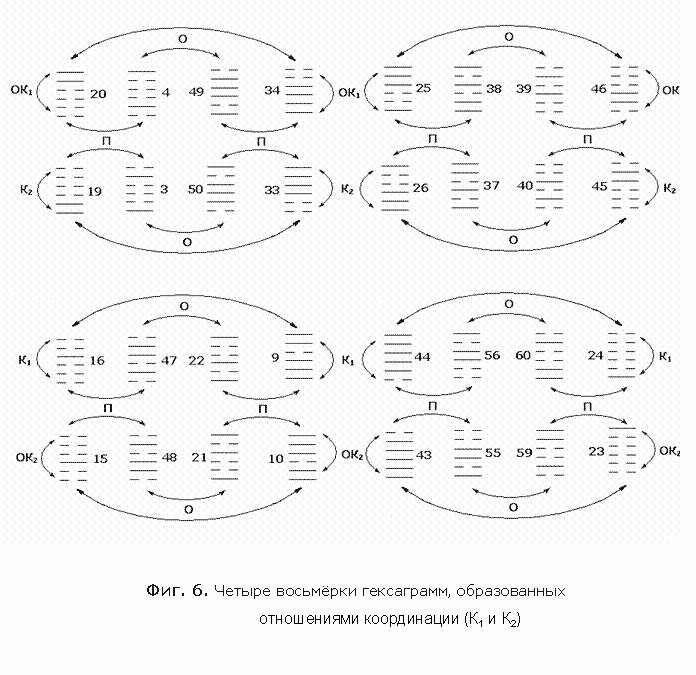
У
нас остаются
шестнадцать
гексаграммВ
образованных
триграммамиВ
стоящими в
отношениях
параллелизма:
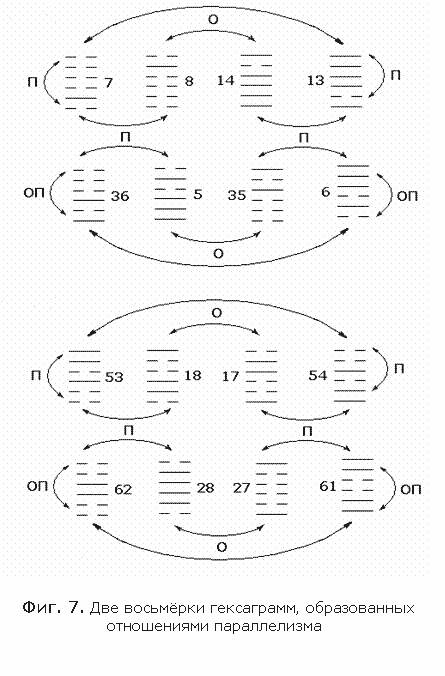
ПонятноВ что
тому же
принципу
следует
распределение
гексаграмм
по лсемействам╗
или лдворцам╗
Цзин ФанаВ
основанное
на отношениях
тождества (А)В
оппозиции (О)В
координации
(К1 и К2)
и
параллелизма
(П) [2]:
![]() .
.
В
каждое из
восьми
семейств
Цзин Фана
входит по
паре
гексаграмм
одной из восьмёрок
вышеприведённых
четырёх
групп по
шестнадцати. При этом
если
тридцать две
гексаграммыВ
построенные
на
отношениях
координацииВ
могли быть
получены
лумножением╗
кардинальных
на
модифицирующие
(Фиг. 5В6)В то к шестнадцати
гексаграммам
Фиг. 7В
образующим
последние
пары в
лдворцах╗ Цзин
ФанаВ этим
путём мы уже
перейти
никак не можем.
Вместе с
тем можно
заметитьВ что
в каждой из
двенадцати
четвёрокВ
расположенных
в
циклическом
порядке Фиг.
5В обнаруживается
по
одной-единственной
гексаграммеВ
от которой
посредством ху гуа
(операции
построения
лвнутреннего
знака╗) может
быть
образована
одна из
четырёх гексаграмм
(27-28 и 53-54)а
заключительной
лгруппы
параллельных╗.
Ху гуа
есть
последнее из
главных симметрических
отношений И цзина:
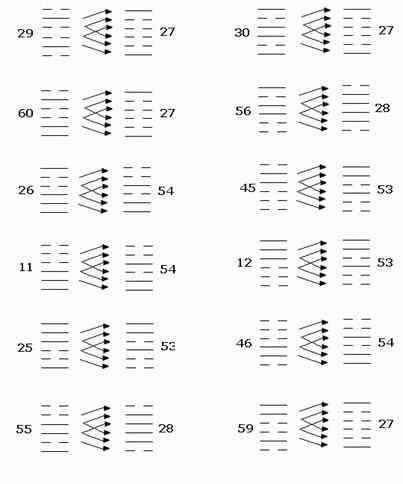
Эти
две пары 27-28 и 53-54 аиз последней
группы Ч
назовём их
кардинальными
II рода Ч
появляются в
круге 12-ти не случайноВ
но отмечают в
нём характерный для
ба гуа и круга
гексаграмм
лпервичный
крест╗ двух
взаимно
перпендикулярных
осей билатеральной
антисимметрии
- Фиг.
8:
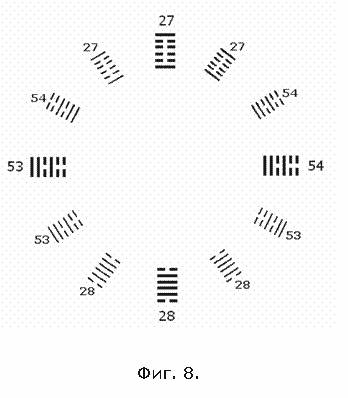
Восемь пар гексаграммВ
образованных
на основе
лпараллелизма╗В
получаются
последовательным
умножением
этих четырёх
лкардинальных
II рода╗ 27-28 и 53-54
на четыре
чистых знака 2В
52В 29а и 57, помещённых
в центре Фиг. 5В
которые выше
мы назвали
лмодифицирующими╗.
Так
порождается
последний
пятый круг
гексаграмм в
шестидесятеричном
цикле, и ещё
четыре знака
сверху (в
музыкальной
системе отвечающие
четырём
дополнительным
бемолям) Ч Фиг.
9:
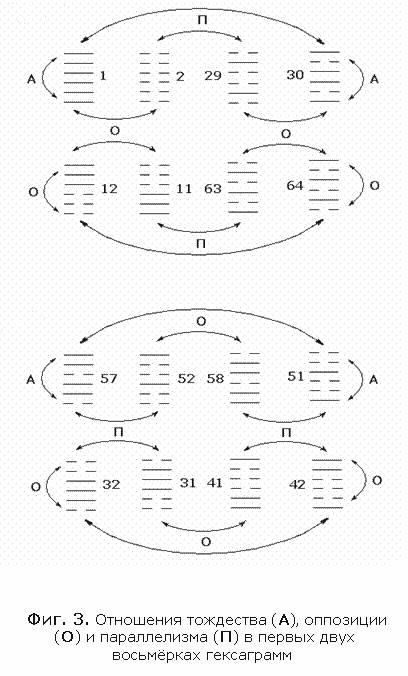
Таким путём
все 64
гексаграммы И цзина
распределены
нами
согласноа правильным
ветрам аквинтовой
музыкальной
системы Ч Фиг.
10. Из нижнего
рисунка
видно, что
найденное расположение
значительно
более
упорядочено,
чем
последовательность
Вэнь-вана:
аааааааааааааааааааааааааааа
ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ааааааа ааааааааа 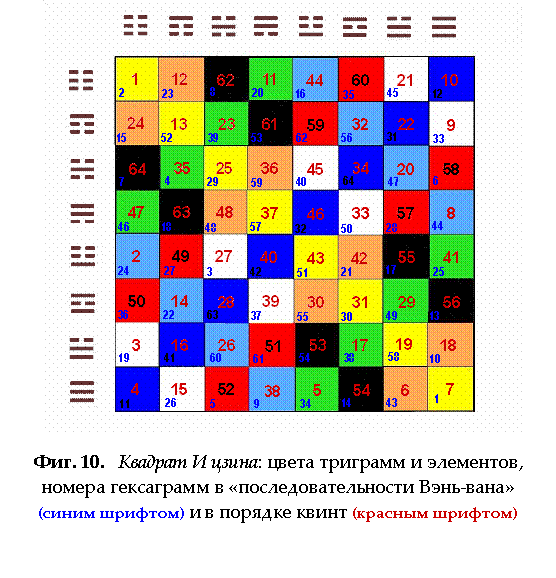
 ааааааааааааааааааааааа ааааааааааааааааааааааааааааааааааааааааааааааааааааааааа аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ааааааааа
ааааааааааааааааааааааа ааааааааааааааааааааааааааааааааааааааааааааааааааааааааа аааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ааааааааа
Хотя
данный
способ не
является
единственно
возможным Ч
очевидно, что
их не так уж
много; и если правильные
расположения
60-ти и 64-х
гексаграмм,
помимо
биномиального
(т.е. в лпорядке
порождения╗),
вообще существуют,
то все они
так или иначе
должны соотноситься
с описанными
выше
симметрическими
свойствами. А
симметрия
эта, как
музыка Ч шестизначна,
кто найдёт в
ней
нарушение:
ааааааааааааааааааааааааааааааааааааааааааааааааааааааааа
ааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ааааааааа 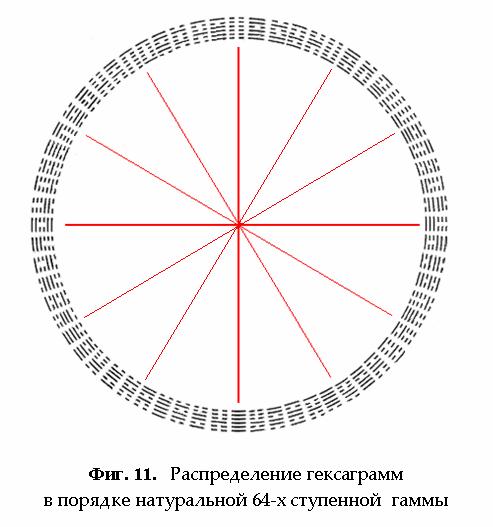 ааааааааааааааааааааааааааааааааааа ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа
ааааааааааааааааааааааааааааааааааа ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа ааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааааа
лПредок Чжуансюй
появился на
свет в реке Жо, а посенлился
на горе Полая
Шелковица.
Когда он стал
преднком-ди
и душой
слился с
небом, подули
правильные
ветры, звуки
их были: си-си,
цзян-цзян
Е Чжуаньсюю
они
полюбились, и
он велел
Летящему
Дракону - Фэйлуну
-
сделать
мелодию в
подражание
этим восьми
ветрам.
Назвал её
лПодносим
облака╗, чтобы
исполнять
при жертвах
Высокому
предку. Потом
велел
Жёлтому угрю
первый раз иснполнить
барабанный
бой; тот
опрокинулся
на спину и
заколонтил
хвостом по
брюху: ян-янЕ╗