Глава 3

                    ОКТАВА

 

 Musika est exercitium arithmeticae occultum nescientis se numerare animi

G.-W.-F. Leibniz

 

  («Музыка есть потаённое арифметическое упражнение души,  не умеющей  исчислить самое себя»)

                                                                           Лейбниц

 

 

 

Итак, мы  удостоверились в том, что пропорции  тетрактиды (1:2:3:4), согласно  Тимею,  служат «гармонической скрепой» космического тела, а значения чисел Октавы, в которых эти пропор­ции проявлены, соотнесены со всем  многообразием возникших вещей,  для  которых  число выступает основной «динамической харак­теристикой», отражающей как порядок возникновения, так и способ отношения с космическим целым.  Этот грандиозный абстрактный план разделённого единства в своей совокупности формирует «тело вре­мени» - той феноменальной  реальности, с которой мы лишь и имеем дело в каждом конкретном случае. Эта  реальность  является  фрак­тальным по­добием  Целого – его  κυνητη εικον  – «подвижной  иконой».

Легко заметить, насколько этот подход – кстати, вовсе не явля­ющийся прерогативой только Платона, давшего «квинтэссенцию» повсе­местно рас­пространённой в древности доктрины, известной сейчас глав­ным образом в одной специфической её форме - «западной Кабалы» - созвучен столь бурно развившемуся сравнительно недавно  фрактально-геометрическому методу анализа нелинейных систем. Естественно, бронзово­му веку не было дела до функционального анализа и компьютерного моделирования, но не порази­телен ли в высшей степени тот факт, что основные черты современного на­учного направления, сместившего акцент от описания мира как уравнения к описанию его как «узора» - паттерна,  создающего в непрерывном разви­тии «узоры» всё возрас­тающей сложности - был парадигматически, в глав­ных чертах и на самой общей основе‚  предугадан в космологических  по­строениях Тимея? Наука заворожена открывшейся перед ней сверхсложностью естественных процессов - но как знать, не есть ли обнаруживаемые ею всё более глобальные закономер­ности лишь отражения, в конеч­ном итоге, паттерна наиболее общего порядка - законов функционирования самого сознания?

Артур Шопенгауэр в “Die Welt als Wille und Vorstellung” (т.2‚ гл.4), предваряя свою таблицу «основных понятий  a priori»,  гово­рит следующее:

 

«Данную таблицу можно рассматривать либо как свод вечных основных законов мира, следовательно, как основу онтологии, либо как главу физиологии мозга, в зависимости от того, приня­та ли реалистическая или идеалистическая точка зрения, хотя в по­следней инстанции правильной окажется вторая»[1].

 

Такого рода следствия естественно проистекали из критических прозре­ний  Канта. В приводимой Шопенгауэром таблице чистых (до опытных) ос­нований познания, пункт 1.1,  читаем:

 

«Существует только одно время, и все раз­личные времена - его части».

И далее (1.8):

«Посредством времени мы считаем»[2].

 

Два этих положения могли бы иллюстрировать учение, развёрнутое Тимеем, но Платон куда более точен:  его число есть форма частного вре­мени (как различия - μὴ ὀν) относительно «Единого» (как тождества - το ἑν). В его космосе пропорция тетрактиды (1/2/3/4) образует паттерн развития, согласованный с «четырьмя элементами» натурфилософии, а  всё последую­щее многообразие мира - «движение» и «дыхание» космоса - есть образуе­мое этим паттерном фрактальное множество значений 3ⁿ/2^m (где n и m свя­заны определённым рит­мом) чисел конкретного времени, отвечающих гармоническим ступеням обобщённой пифагорейской октавы.

 

Эту числовую систему в своих наиболее характерных чертах мы хотим предоставить вниманию читателя в качестве обзора музыкального строя‚ из­вестного как квинтовый или пифагорейский строй, - легко опровергающего укоренившееся  от начала «века просвещения» и широко распространённое до сей поры мнение, что «совершенная математическая система музыкальной гармонии невозможна»[3]. Более того, оказывается, что «гармоническими скрепами» связываются - теоретически - любые два числа, только количество требуемых для этого  шагов  может быть большим или меньшим. Здесь же мы вовсе не касаемся метроритмической организации музыки - компонента её не менее значимого‚ чем звуковысотный состав:

 

         «Мелодия состоит из двух элементов‚ ритмического и гармонического; первый можно назвать также количественным‚ второй качественным... Ритмический элемент наиболее существенен‚ так как он сам по себе без помощи другого элемента может создать некое подобие мелодии‚ что и происходит‚ например‚ на барабане; полная же мелодия требует того и другого. Она состоит в меняющемся разъединении и примирении обоих»;

 

         «подобно тому как в архитектуре регулирующим и объединяющим началом служит симметрия‚ в музыке таковым является ритм»[4].

 

 

Каждому изучавшему элементарную теорию музыки хорошо известно, что все ноты гаммы могут быть образованы ходами в квинту, если от исходного тона, принятого за основной, брать пятые ступени (вверх либо вниз), и  получаемые звуки сводить в исходную октаву,  понижая либо повышая их на восемь ступеней. Тем, кому это ничего не говорит, мы попытаемся сей факт как можно убедительнее продемонстрировать, что называется, «на пальцах»; поразительно то, что знанием вышеупомянутого факта, в основном, и ограничивается  представле­ние о пифагорейском натуральном строе даже музыкальных специалистов. А ведь именно ему - как станет ясным из дальнейшего - обязана му­зыка важнейшими своими «материями»: семиступенным ладом‚ двена­дцатиполутоновой  гам­мой  и  т.п.

До той поры, как темперированный строй вошёл в широкое употребление (т.е. до времён Баха)‚  в основу музыки были положены отноше­ния  консонансов, и её «пифагорейская природа» пред­ставлялась куда как более очевидной.

Шестнадцатое столетие ознаменовалось всплеском интереса к музыкальной акустике - как столетием-двумя ранее «титаны возрожде­ния»  увлекались геометрией и экспериментиро­вали в области перспективы в живописи. Именно Галилео Галилею и францисканскому монаху Марену Мерсенну (внесшему свой вклад также в развитие теории чисел) приписывается открытие закона гармонического колебания струны, - при котором частота колебания обратно пропор­циональна длине струны. Впрочем, сей  факт на монохорде Пифагора мог бы  продемонстрировать уже и Эвклид в III в. до н.э. в приво­димом ниже опыте[5].

 Мерсенном был также описан обертоновый ряд - после­довательность частот свободных колебаний струны, соотносящихся как це­лые числа 1:2:3:4:5... Начальная фаза волны укладывается по всей длине струны, эта деформация порождает вторую волну, укладывающуюся двумя фазами, затем  - тремя и так далее, что в сумме даёт единое звуковое впе­чатление (высоту и тембр) звучащей струны - Фиг. 3.1.

Первый обертон (2) есть гармонический интервал октава,  второй обер­тон (3) - гармонический интервал квинта, с четвёртым уже возникает то­ническое трезвучие (до-ми-соль), двенадцать обертонов  дают  полную семи­ступенную гамму. Обертоновый ряд заключает в себе первый и наиболее общий закон гармонии - вся музыка, в принципе, могла бы уже основываться на нём одном[6]. Но второе необходимое условие, как мы убедимся в дальнейшем, есть требование подобия части целому - с тем, чтобы  система фиксированного звукоряда  стала возможной[7].

Вопрос о природе консонанса, или почему одни звуки при сочетании создают при­ятное (гармоничное), а другие - неприятное (диссонантное) ощущение находит объяснение в явлении обертона: когда длины двух струн связаны простыми числовыми отношениями – 2:1 (октава), 3:2 (квинта), 4:3 (кварта) и проч., то порождаемые ими колебания будут иметь сов­падающие звуковые частоты.  В случае настройки в октаву основной тон второй струны будет первым обертоном первой струны, в квинту  - вторым оберто­ном,  в кварту - второй обертон второй струны будет третьим обертоном первой, и т.д. Или же, сказать иначе, чем ближе основные частоты двух носителей колебаний к простому отношению, тем больше фазовых совпадений  - кон­сонансов -  возникает между ними, чем оно дальше‚  тем больше проявляется разност­ных тонов - определяемых как разность основных частот, а также  разности обертонов, - низкочастотных «биений», придающих звуку «шероховатость». Эти выводы был сформулированы Германом Гельм­гольцем в середи­не девятнадцатого века в его «Учении о слуховых ощущениях» (1862).

 

Открытия европейских ученых только послужили подтверждением тех теоретических представлений что‚ как мы знаем‚ были известны гораздо раньше в древней Гре­ции, а равно  в  Индии  и  Китае.

 

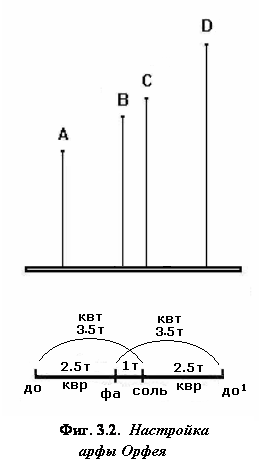Рассмотрим так называемую «настройку арфы Орфея»  и эксперимент, связываемый с именем Пифагора. Обучавшие музыке пифагорейцы демонст­рировали на опыте, что три струны, натянутые на общей основе‚  резонируют при соотношении их длин 2:3:4. При этом возникают  гармонические со­звучия октавы - 1-я и 3-я струны, квинты  - 1-я и 2-я струны‚  и кварты  - 2-я и 3-я струны.  В настройке  арфы Орфея  добавлялась ещё  четвёртая - про­межуточная - струна, обра­зующая, обратно, кварту с первой и квинту с последней  струнами (т.е.  верхним и нижним пределами интервала в октаву).  При этом две средние струны создают интервал целого тона (9:8). Продолжая эту процедуру, т.е. построив октаву  на средней струне и подобрав  квинту в новой  октаве, мы получим следующую  ступень гаммы  и так далее, пока не завершим весь звукоряд - Фиг. 3.2.

       Это соотношение четырёх струн - тетрахорд - задавало основное правило  - гно­мон - натурального строя античной музыкальной сис­темы.

 

Вполне вероятно, что древним грекам было удобнее строить звукоряд от  си – то есть квинтами вниз, но мы воспользуемся более привычным для нас способом и другой последовательностью ступеней. Назовём исходный тон  фа (на самом же деле  им может быть любой).

Квинта от фа вверх будет до¹ (следующей ок­тавы). Опустим это до¹ на октаву вниз. Если началь­ную фа принять за 1, то до¹ или квинта есть 1х3/2=3/2, а до в исходной (т.е. малой) октаве отно­сится к до¹ как 1:2, по­этому ступень до получает зна­чение 3/2:2=3/4 и есть кварта к фа – обра­щённая квинта.  Квинтой  от до=3/4 вверх будет следующая ступень, «зер­кально-симметричная» к фа, т.е. соль=3/4х3/2=3²/2³=9/8. Мы видим, что коль скоро исходный тон фа получил значение единицы, все образуемые квинто­выми ходами величины будут значениями интервалов относительно фа. В данном случае вторая квинта (3²) порождает интервал целого тона (9/8). Но с  верхним до¹ ступень соль образует кварту (обратную квинте относительно интервала октавы):  до¹/соль = 3/2 : 9/8 = 4/3.

Порождённая двумя квинтами и двумя квартами в пределах октавы   четверица  до-фа-соль-до¹ с отношением частот  1 : 4/3 : 3/2 : 2  есть основа всех гармонических музыкальных соответствий и аналогична «настройке арфы Орфея» (e¹-h-a-e); она же отвечает  пропорции космических элементов платонова Тимея как выражению пифагорейского тетракса. На этом моменте вследствие его особой значимости можно  остановиться чуточку под­робнее. В данное выражение входят все известные пропорциональные отношения, а именно арифметическая, геометрическая и гармоническая прогрессии, а также принцип золотого деления. Закон золотого деления гла­сит, что меньшая часть так относится к большей, как большая часть  -  к целому, и в нашем случае наименьшая часть, полученная  при делении интервала октавы - 1 тон  (9/8) так относится к большей части - квинте,  как последняя от­носится к октаве: 9/8 : 3/2 =3/2 : 2 =3/4. Далее, 3/2 есть среднее арифметиче­ское 1 и 2, 4/3 - среднее гармоническое 1 и 2, а вместе и среднее арифмети­ческое 2/3 и 2. Сам квинтовый способ образования ступеней умножением на 3/2 есть геометрическая прогрессия[8]. Квинта  относится к кварте как октава (3/2:4/3=2),  а квинта  к 1 тону  ─  как кварта (3/2 : 9/8 = 4/3). На основании этих закономерностей связываются пропорциями и все последующие нисхо­дящие интервалы, основанные на тройственном делении четверицы.

 Напомним, что отношения пропорции 1:2:3:4 соединяют между собой и  геометрические элементы пяти правильных многогранников - платоновых тел (дополняясь в случае икосаэдра и додекаэдра пятёркой[9]).

 

Продолжим далее наше построение. От полученной второй квинтой ступени соль отложим вверх следующую квинту: 3²/2³х3/2=3³/2⁴. Эта ступень соответствует ре¹ следующей, т.е. первой октавы (3³/2⁴>3/2=до¹), поэтому мы понижаем её в исходную октаву (как ранее поступили с до¹), т.е. делим на два: 3³/2⁴:2=3³/2⁵ или 27/32 – это интервал малой терции (вниз от исходной фа). Квинта вверх от ре есть 3³/2⁵х3/2=3⁴/2⁶ или 81/64 и соответствует ля той же (малой) октавы и интервалу большой терции  (вверх от фа). Заметим, что показатель степени 3 для каждого интервала соответствует номеру квинты, посредством которой этот интервал был получен.

Пятой квинтой, взятой от новой ступени ля вверх, или 3⁴/2⁶х3/2=3⁵/2⁷ будет ми¹, и её мы сводим в исходную октаву: 3⁵/2⁷:2=3⁵/2⁸ - это интервал диатонического полутона (вниз от фа). Шестая квинта‚ взятая от ми‚ составит 3⁵/2⁸х3/2=3⁶/2⁹ и соответствует си малой октавы, завершая семь «основных ступеней» (вме­сте с исходной),  образованных  в следующем порядке:

 

 

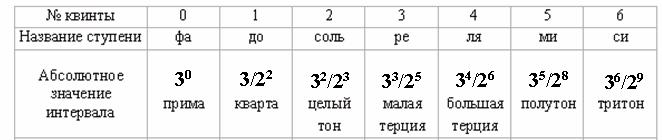
Поскольку ряд ступеней был понижен на октаву с тем, чтобы занимать положение в одной октаве с фа, некоторые значения интер­валов оказались меньше единицы, то есть лежащими ниже  фа: до=3/4<1, ре=27/35<1, ми=243/256<1. Три другие ступени располагаются выше фа, по­скольку значения их интервалов превышают единицу: соль=9/8>1, ля=81/64>1, си=729/512>1. Все полученные ступени заключены в пределах между до=3/4 и до¹ =3/2 -  или  в октаве до-до¹.

Между ступенями‚ расположенными в порядке  высотного возрастания‚ разностные интервалы следующие:

 

ре-до =3³/2⁵:3/2²=3²/2³ =9/8,

ми-ре =3⁵/2⁸:3³/2⁵=3²/2³ =9/8,

фа-ми =1:3⁵/2⁸=2⁸/3⁵ =256/243,

соль-фа =3²/2³:1 =9/8,

ля-соль =3⁴/2⁶:3²/2³=3²/2³ =9/8,

си-ля =3⁶/2⁹:3⁴/2⁶=3²/2³ =9/8,

до¹-си =3/2:3⁶/2⁹=2⁸/3⁵ =256/243.

 

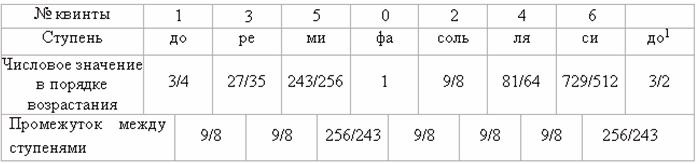
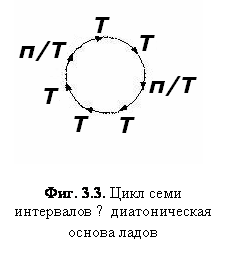
Полученная шестью квинтами семиступенная октавная гамма с разделе­нием на 5 интервалов в 1 тон (9/8) и 2 полутоновых интервала (256/243) в последовательности ТТп/тТТТп/т соответст­вует натуральной диатонической (мажорной) гамме основных музы­кальных ступеней  (Фиг. 3.3.).

 

 

Как можно заключить из вышеприведённого расчёта, семиступенная диатоника явля­ется математическим  фактом, вытекающим из природы пропорции 1 : 4/3 : 3/2 : 2 (квинтово-квартового деления октавы). Музыкальный  авангардизм  существенно поколебал представление о «нерушимости» лада (лежащего, как известно, в основе тональностей) - ведь  разделе­ние октавы  на семь частей  лишь одна из многих возможно­стей. Тем не менее, семь диатонических ступеней и тональности  - не просто «дань  традиции» или тем более «вкусу», но имеют прямое отношение к пред­мету: если живопись вообще может быть «нефи­гуративной», то и атональность в му­зыке, оче­видно, должна как-то намекать на то, что именно отсутствует.

Отметим ещё для сообразительного читателя: если  промежуток ок­тавы, как нами было только что установлено, поделён на семь основных ступе­ней,  то  самая октава (с двумя до ─ нижним и верхним) слагается восемью (окта есть восемь) ступенями -   2³.  

Два основных консонансных - поскольку они являются ближайшими оберто­нами - отношения 3:2 (квинта) и 4:3 (кварта) при их  «сложении»  (а в музыке сложение интерва­лов есть умножение их высотных отно­шений, основанное на сквозной про­порциональности вида Д/А=Д/С х С/В х В/А) дают интервал октавы‚ равный 2, поскольку  3/2 х 4/3 = 2. Два - бли­жайший обертон‚ и он с необходи­мостью вытекает из самой природы волнового движе­ния, выражаемого гармониче­ской кри­вой  - Фиг. 4.1.

Гармоническая кривая - как свиде­тельствуют математика и физика - суть наиболее общий закон движения: ко­лебаниями или волновыми процессами описываются электромагнитные волны (свет), состояния электронов в ато­мах, природа  микрочастиц‚  а также движения в простран­стве – от качания листа до об­ращения планет. Уравнения классической механики могут быть представлены в виде сумм гармониче­ских кривых  посредством раз­ложения в ряды Фурье. В современном направ­лении синергетики компью­терное моделирование сложных (нелинейных) процессов различной природы - качест­венный функциональный анализ диффе­ренциальных уравнений  - приводит к фи­гурам тем или иным образом связанных циклов как к «конеч­ным решениям» не­предсказуемых иным способом так назы­ваемых «хаотиче­ских систем».

Учитывая сказанное‚ вовсе не удиви­тельно, что в природе музыки  (кото­рую обычно склонны рассматривать только как эстетический фено­мен), осно­ванной на физическом явлении - волновом колебании воздушной среды - также прояв­лено основное числовое свойство гармони­ческой кривой, а именно – её свойство двой­ственности. Это было известно и древним (в этой книге мы говорим лишь об из­вестных вещах), обозначавшим неорганизо­ванную мировую субстанцию - первоматерию или «потенциальный ва­куум»  (ὔλη - «хюле»)  двоицей,  которая с тем‚ чтобы  обнаружить свои проявленные‚ т.е. энергетические свойства‚  должна быть расчленена -   численно органи­зована  оп­ределённым способом‚ в нашем случае -  делением   3:2  или сле­дующим за окта­вой обертоном.  Архаический миф орфи­ческой религии гласит следующее:

«Ночь выносила Луче­зарное Яйцо. Фанет (он же Брахма – «первородный»)‚ выйдя из  Яйца (сингулярно­сти), расколол  его на  две по­ловины - Небо и Землю‚ породив начало всех бо­гов» (1+2=3).

 

В этом же смысле говорит первый стих первой главы книги Бытия:

                              «В начале сотворил Бог небо и землю».

 

Этим отступлением мы вновь акцентируем внимание на онтологических корнях музыки – как в её непосредственном отношении к теории числа и основаниям физики и математики, так и в том особенном мировоззренческом значении, которое ей придавалось  эзотерической  традицией древних [10].

Возвращаясь к анализу музыкальной гаммы, мы должны отметить и то, что паттерн или отношение четверицы 1 : 4/3 : 3/2 : 2 (кварты, квинты и октавы) повторяется для любых ступеней, взятых в последовательном порядке:

 

 

                                                                                     

                      

 

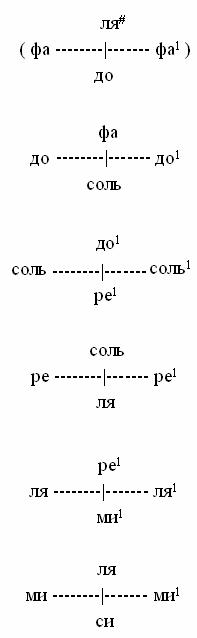
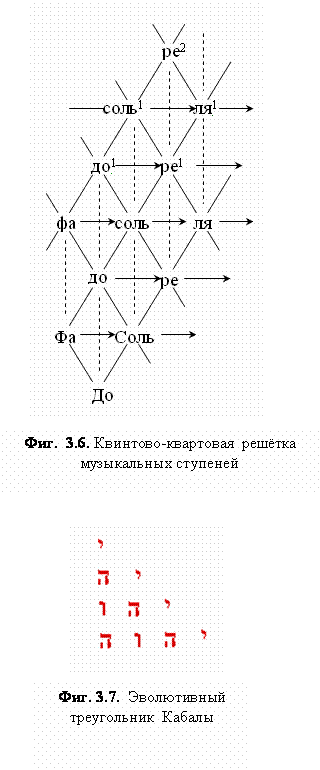  В этих «схемах порождения» роль ок­тавы (соответствующей тонике), делимой квин­той и квартой - то есть «пассивного элемента» - берёт на себя ступень, полученная на предыду­щем этапе (как доминанта), а роль «активного (делящего) элемента» - та ступень, что выполняла роль октавы на предыдущем этапе (как субдоми­нанта). Так, в октаве до-до¹ интервал  фа-до¹ - квинта в предшествую­щей октаве фа-фа¹, а вновь получаемая ступень соль («уравновешивающий элемент») образу­ется симмет­рично к фа квинтой до-соль:  как бы зеркальным отражением предыдущей квинты от ступени  до (Фиг. 3.2). Между средними членами («порождающим» и «порождён­ным») всегда лежит интервал целого тона (9/8).

Мы  подробно останавливаемся на этих (очевид­ных для музыкантов) об­стоятельствах для того, чтобы уяснить здесь далеко уводящую от собст­венно музыки параллель. Поря­док порождения ступеней соответствует так называемым эволю­тивным тер­нерам Кабалы, составленным из букв Неска­зуемого Имени (тетраграмма­тона), а их подразделение на «пассивный»‚ «активный» и «уравновешивающий»  отвечает  трём гунам - принципу, как будет пока­зано ниже, носящему  вполне универсальный характер.

 «Активный элемент» (Йод (י) - «отец»), нала­гаемый на «пассивный элемент» (Хе (ה) - «мать»), порождает третий или  «уравновешивающий эле­мент» (Вау (ו) - «сына» либо «дочь»),  записываются справа налево (Фиг 3.7.). В следующей по порядку триаде «пассивный» элемент ставится на место «активного» (Хе®Йод), а «уравновешивающий» - на место «пассив­ного» (Вау®Хе). Пять таких нисходящих тетрад - в числе равных пяти элемен­там природы или  пяти «творческим светам» - расчленяют «пустое пространство» двоицы (Октавы) с образованием семи промежутков и шести промежуточ­ных ступеней;  «размерил Вселенную в шесть шагов», как гласят индийские шастры:

 

                     «Я есмь Отец и Мать, я – также Сын;

                     Я есмь душа всего что есть, что было

                      И что будет»

                                                                    (Махабхарата 5. 45. 24-28).

 

В чисто-математическом плане это указывает на определённый симмет­рический рисунок (паттерн) - повторенный, как мы увидим в дальнейшем, на всех уровнях строения Октавы.

 

Приводимая (эзотерическая) трактовка четверицы  как генетической ос­новы семитонового разделения октавы-двоицы может быть дополнена  двумя сле­дующими числовыми построениями (Фиг. 3.8 а,б). Первое из них следует порядку треугольной Фигуры 3.7., второе включает четыре «четвёрки» (№№ 1-7) полной диатонической гаммы. Интересно, что в первом случае (а) сумма входящих цифр есть удвоен­ная декада (2х10=20) или  виналь, во втором случае (б) она составляет 64 (2⁶) – число Пере­мен И цзина (!) Если же  мы возьмём числовые значения букв Фигуры 3.7. -  а именно,  י=10, ה=5,  ו=6, то их сумма будет 72 - Шем  хамфирош  Несказуемого Имени или  пятая часть от 360-ти ( см. об этом ниже).

 

Очевидно, что шесть квинтовых ходов вверх от фа не исчерпывают всех  ступеней гаммы; этот процесс может быть продолжен и далее двояким способом. Мы можем продолжать наращивать квинты  вверх от си, а можем  опускать их от исход­ной ступени фа вниз, получая новые значения интерва­лов. Проследуем  же обоими  этими  путями.

Квинта вверх от си=3⁶/2⁹  (по счёту седьмая) составит интервал 3⁷/2¹⁰, поскольку же она приходится на  следующую октаву (превышая до¹=3/2), это значение  должно быть разделёно на 2, что в исход­ной октаве даёт 3⁷/2¹¹. Подобным  образом получаются и следующие ступени:

                                                          VIII квинта  3⁷/2¹¹х3/2=3⁸/2¹²>3/2,

     поэтому 3⁸/2¹²:2=3⁸/2¹³;

                                                          IX квинта   3⁸/2¹³х3/2=3⁹/2¹⁴;

                                                          X квинта    3⁹/2¹⁴х3/2=3¹⁰/2¹⁵>3/2,

                                                               поэтому 3¹⁰/2¹⁵:2=3¹⁰/2¹⁶;

                                                          XI квинта   3¹⁰/2¹⁶х3/2=3¹¹/2¹⁷;

                                                          XII квинта  3¹¹/2¹⁷х3/2=3¹²/2¹⁸>3/2,

                                                               поэтому 3¹²/2¹⁸:2=3¹²/2¹⁹.

 

Седьмая квинтовая ступень ниже на полутон (2⁸/3⁵) ступени  соль: 3²/2³ : 2⁸/3⁵ =3⁷/2¹¹, поэтому она  получает значение соль, пониженной на полтона (соль^b). Восьмая квинта даёт пониженную на полтона ре, так как 3³/2⁵:2⁸/3⁵=3⁸/2¹³ (соответствует ре^b), девятая, точно так – ля^b (3⁴/2⁶:2⁸/3⁵=3⁹/2¹⁴), десятая – ми^b (3⁵/2⁸:2⁸/3⁵=3¹⁰/2¹⁶), одиннадцатая – си^b (3⁶/2⁹:2⁸/3⁵=3¹¹/2¹⁷). Наконец, двенадцатая квинта должна прийтись на по­ниженный на полтона интервал седьмой ступени, поскольку 3⁷/2¹¹ (соль^b): 2⁸/3⁵=3¹²/2¹⁹. Что же это за новая ступень соль^bb с двойным бемолем?

Каждый, кто имел дело с нотными обозначениями в современной трактовке (т.е. равномерного темперированного строя) скажет, конечно, что это ступень фа, но в пифагорейском натуральном строе два пол­утона (дубль-бемоль) не дают интервала, равного целому тону (2⁸/3⁵х2⁸/3⁵=2¹⁶/3¹⁰<9/8), равно как и полученное значение интервала соль^bb 3¹²/2¹⁹=531441/524288 =1.0136432 превышает единицу - интервал  примы (3⁰). Приняв во внимание эти два соображения мы должны признать, что двенадцатая квинта вверх от исходной ступени фа=1 порож­дает  малый интервал 3¹²/2¹⁹  больший примы‚  и численно соответствующий разнице интервала целого тона  и двух полутонов:  3²/2³:(2⁸/3⁵)²=3¹²/2¹⁹, что составляет примерно 1/8,69  целого тона (или, как можно ещё записать, 1.0136432^8,69=9/8).

Этот микроинтервал, который мы будем обозначать значком Δ («дельта»), известен под наименованием «пифагорейской коммы»‚ и в музы­кальной теории определяется как «разница между исходным тоном и двена­дцатой квинтой вверх при сведении в ту же октаву».

«Наличие коммы ведёт к акустическому недостатку»‚ - говорит  руководство по настройке инструментов. Различие по высоте в 1/9 тона вряд ли уловимо на слух при раздельном звучании двух звуков (находится в пределах «зоны»), но при одновре­менном исполнении оно порождает «шероховатость» (низкочас­тотное биение). Присутствие же биений, как известно, уже изначально заложено настройкой в темперированном строе[11]. Этот и прочие «недостатки», равно как и сравнительные особенности различных строев мы попытаемся вкратце рассмотреть ниже (Приложение 2). Пока же лишь заметим, что приводимый нами здесь расчёт квинтовой музыкальной системы вызван, строго говоря, не  узко-музыкальными задачами - хотя и имеет самое прямое отношение к выяснению природы музыки: ­он определяется той  ролью, которую этой числовой системе придавало учение древности. Далее будут выявлены интригующие параллели между музыкальной онтологией пифагорейцев, рассматривавших гармонию в качестве чисто-дедуктивной теории, выводимой из общего принципа (наравне с геометрией)‚ и число­выми моделями времени в космологиях древнего мира.

 

Полученная нами последовательность интервалов из двенадцати восхо­дящих квинт (Фиг. 3.9.) есть не что иное, как

 

 

хорошо известный «квинтовый круг» тональностей -  или, говоря более точно, «квинтовая спи­раль». Но в обозначении современной европейской музыки (основанной на замкнутом строе равномерной темперации, в котором полутон в точности равен половине тона и пониженная ступень может быть заменена равной ей повышенной) в восходящих квинтах вместо ступеней бемоля как дань тёмной традиции фигурируют ступени диеза (вместо соль^b - фа^#‚ и т.д.)‚ а в нисходящих квинтах  - обратное‚ что при общем неведении относи­тельно оригинальной системы способно вконец спутывать карты.

Прежде чем всмотреться более пристально, что же представляет из себя этот «квинтовый круг» и лучше уяснить его структуру, придадим ему симметричность путём построения нисходящих квинт.

Первая  квинта вниз от ступени фа (поскольку теперь мы пони­жаем значение на квинту,  это означает не умножение, а деление на 3/2 - или, что то же самое, умножение на 2/3) есть 2/3 х 2 = 4/3 или 2²/3:  поскольку  эта ступень приходится на нижележащую октаву До (2/3<3/4)‚ то для  её приведения в исход­ную октаву значение 2/3 должно быть умножено на 2. Полученная ступень образована интервалом на пифагорейский полутон выше ля=3⁴/2⁶, поскольку  3⁴/2⁶х2⁸/3⁵=2²/3,  поэтому она соответствует  ля^#.

Вторая нисходящая квинта 2²/3х2/3=2³/3² на полтона выше ре=3³/2⁵:

3³/2⁵х2⁸/3⁵=2³/3²,  и получает обозначение ре^#.

Далее  продолжаем аналогично:

III квинта   2³/3²х2/3=2⁴/3³<3/4 даёт

2⁴/3³х2=2⁵/3³ (=соль^#);

IV квинта   2⁵/3³х2/3=2⁶/3⁴ (=до^#);

V квинта    2⁶/3⁴х2/3=2⁷/3⁵<3/4 даёт

                                                                                     2⁷/3⁵х2=2⁸/3⁵ (фа^#);

                                                                   VI квинта  2⁸/3⁵х2/3=2⁹/3⁶<3/4 даёт

2⁹/3⁶х2=2¹⁰/3⁶ (ля^##).

 

Обратим внимание, что все получаемые нисходящими квинтами альтерированные ступени отличаются от построенных восходящими квинтами -  при­ходящихся на те же номера двенадцатичленного круга - на интервал коммы.  Например,

си^b/ля^#=3¹¹/2¹⁷:2²/3=3¹²/2¹⁹,

ми^b/ре^#=3¹⁰/2¹⁶:2³/3²=3¹²/2¹⁹,  и так далее.

         В полном согласии с этой закономерностью, интервал  шестой квинты вниз от фа  2¹⁰/3⁶ (ля^##) принимает значение пониженной на комму ступени си =3⁶/2⁹, поскольку

3⁶/2⁹:2¹⁰/3⁶=3¹²/2¹⁹, и поэтому мы обозначаем её си^Δ-  - так же как ранее увеличенная на комму фа получила обозначение фа^Δ+.

 

        

 

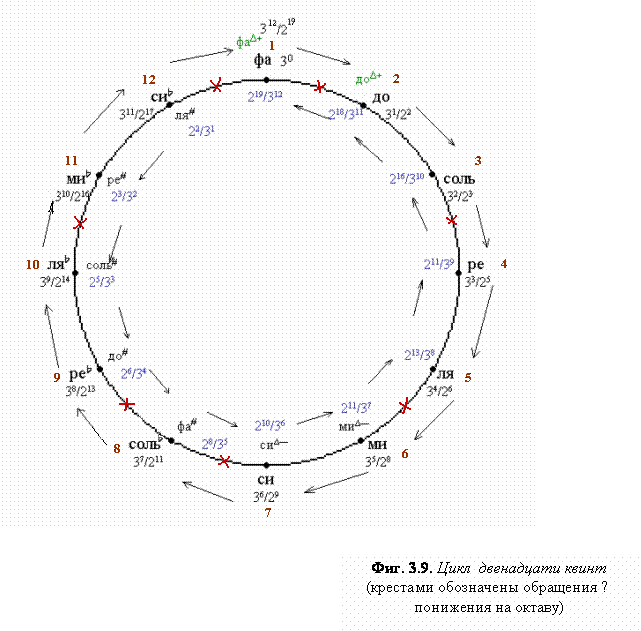
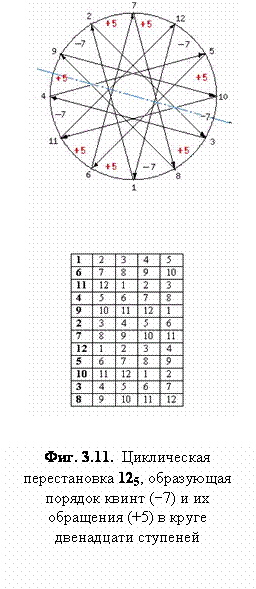
Полученные  результаты  заключают в себе много большее, чем просто разделение октавы на двенадцать полутонов. Не будет пре­увеличением сказать‚ что порождаемый квинтами 12-ти ступенный цикл (Фиг. 3.10. а-д) являет чудо совершенства формальных свойств‚ нисколько не уступая в этом  известным платоновым телам (правильным пространственным многогранникам) - с тем отличием‚ что последние представляют собою статичные‚ а октава - динамически разворачивающуюся структуру.

 

         Все построенные числа интервалов связаны между собой единой систе­мой пропорций: она не столь проста, как на первый взгляд, поскольку  мы переводили предыдущую ступень то на квинту (3/2 или 2/3), то на обратную ей кварту (3/4 или 4/3), порождая неравномерную числовую последовательность в пределах двух крайних значений октавы – от нижнего до = 3/4  до верхнего до¹ = 3/2.

 Этими операциями задаётся нелинейный про­цесс итеративного отображения - подобный тем, что используются во фрактальной геометрии:

                                       х → 3/2 x    при x<1,

                                               х → 3/4 x     при x≥1      (1).                                

  Ниже мы покажем, что процедура квинтовых итераций  в самом деле создаёт фрактальную пау­тину в интервале октавы, характеризующуюся ре­гулярными циклами и повторяющимися паттер­нами.

 

Чередование квинты и кварты в двенадцати­ступенном круге описывается закономерностью, являющейся ни чем иным, как перестановкой две­надцать по пять (12)₅ -  Фиг. 3.11.

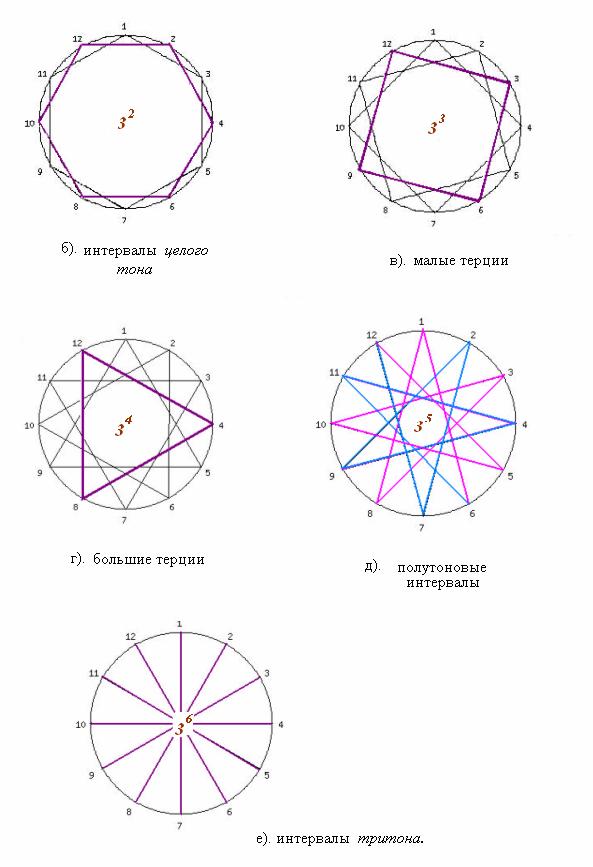
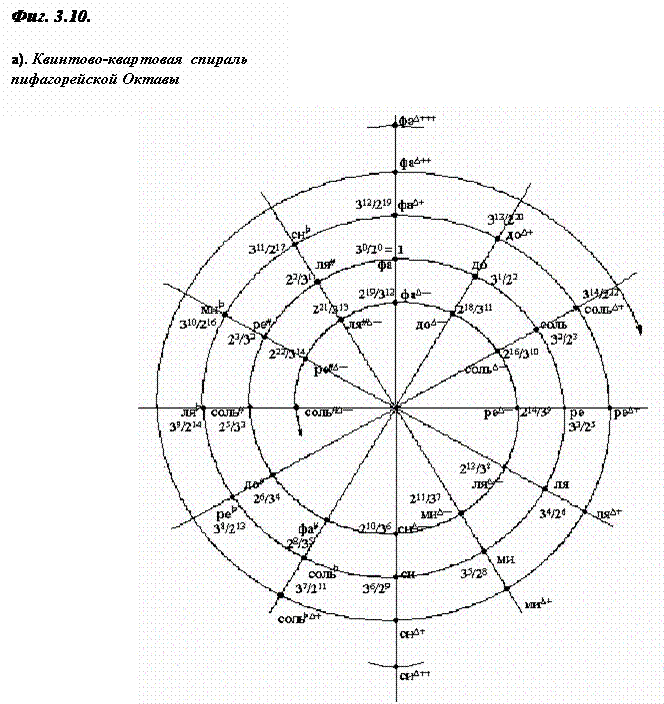Далее, все значения интервалов относительно фа=1 вида 3ⁿ или 3^-n, делённых или умноженных  на 2^m (где n и m связаны упомянутым перестановочным законом), определяя ступени звукоряда, в свою очередь образуют между собой разностные интервалы, выражаемые  частными от деления чисел двух ступеней:

 

1)  3¹  - интервалы  квинты  и  кварты  (3.5 и 2.5 тона) между соседними  номерами круга;

2)  интервалы 3² - отвечающие целому тону (1 тон)‚ через один номер;

3)  интервалы 3³ - соответствующие малой терции (1,5 тона)‚ через  каж­дые два номера;

4)     интервалы 3⁴ - соответствующие большой терции (2 тона)‚ через каж­дые три номера;

5)     интервалы  3⁵  через каждые четыре номера дают полутоновые интер­валы  (0.5 тона) - или, точнее, пифагорейские «лейммы» (см.);

6)     интервалы 3⁶  через каждые пять номеров  - располагающиеся по диа­метрам круга - отвечают интервалу тритона (3 тона)‚ или «увеличенной кварте» (= «уменьшенной квинте»).

 

         Обозначение разностных интервалов степенью числа 3 (или просто разно­стью номеров двух ступеней) - как мы сейчас увидим, позволяет обобщить  различия «интервалов полученных квинтами вверх от фа» и «полученных квинтами вниз от фа», когда числитель и знаменатель  меняются местами, а также все обраще­ния основных интервалов, отличающиеся на единицу в показателе степени  2.

Указанные шесть основных интервалов (не включая  седьмой - приму 3⁰, а также обращения) образуются первыми шестью квинтами и исчерпывают собою практически все используемые интервалы «реальной музыки». Уже седьмая квинта (соль^b) порождает новый разностный интервал 3⁷/2¹¹ относительно №1 фа - заметим, что все  остальные интервалы между ступенью №8 3⁷/2¹¹ и №№ 2-7  остаются в числе упомянутых шести. Этот седьмой интервал, как  легко за­метить, есть «увеличенный полутон» (фа-соль^b) - или  полутон 2⁸/3⁵, повышенный на комму 3¹²/2¹⁹:

                                       2⁸/3⁵х3¹²/2¹⁹=3⁷/2¹¹ (вверх от фа).

Следующая   ступень 3⁸/2¹³, соответствующая  ре^b, даёт разностный ин­тервал 3⁷/2¹¹ с №2 до =3/4, а также и новый интервал с фа - «уменьшенная малая терция» (т.е. 1.5 тона за вычетом  коммы):

                                               3⁴/2⁶ : 3¹²/2¹⁹=2¹³/3⁸  ( вниз от фа)‚ и т.д.

Все изменённые на микротон интервалы располагаются зер­кально-симметрично относительно шести основных интервалов по оси симметрии  №1 – №7 (фа-си):

                            кварта – тон – м.терция – б.терция – полутон – тритон –

 полутон^Δ+ –  б.терция^Δ-– м.терция^Δ+ – тон^Δ- – кварта^Δ+  (Фиг. 3.12.).

 

Ступень №13 фа^Δ по завершении XII квинты или интервал 3¹²/2¹⁹ можно обозначить как «увеличенную приму». Помимо этих 12-ти разностных ин­тервалов (шесть основных и шесть «изменённых основных») - как можно убе­диться, других ступени первых 12 квинт между собой не образуют. Так, на­пример, интервал  ре^b-си  3⁸/2¹³:3⁶/2⁹=3²/2⁴  не отличен от 3²/2³: он есть малая септима или обращенный интервал целого тона: 3²/2³ от си вверх дает значение ступени ре^b1, нуждающейся в сведении в исходную октаву, т.е. де­лении на 2. Кажущиеся новыми разности, по-сути, не определяют никаких иных ин­тервалов помимо вышеперечисленных двенадцати, но получаются «за выче­том» ранее полученных из интервала октавы‚ равного 2.

 Интервал между №13 и №7  фа^Δ-си 3¹²/2¹⁹:3⁶/2⁹=3⁶/2¹⁰ есть «уменьшен­ный на Δ тритон», численно равный обращённому тритону (2⁹/3⁶:2) поскольку, как мы уже знаем, натуральная октава не со­стоит из двух тритонов (3 т. + 3 т.), но меньше шести тонов на комму  Δ (интервал 2 = 6 т/Δ). Иначе говоря, два последовательно взятых тритона при сведении в ту же октаву дают комму:

 

                                                                                                                                      3⁶/2⁹ х 3⁶/2⁹ : 2 = 3¹²/2¹⁹.

 

При понижении квинт, то есть при движении по квинтовой спирали  влево от №1 фа‚ получаются  такие  интер­валы:

1)     первая квинта вниз от фа образует ступень 2²/3 - т.е. кварту (обращён­ную квинту) вверх;

2)     вторая квинта  даёт 2³/3² – тоновый интервал, взятый вниз от фа;

3)     третья  квинта  есть 2⁵/3³  - малая терция вверх от фа;

4)     четвёртая  - 2⁶/3⁴ - означает большую терцию вниз;

5)     пятая квинта 2⁸/3⁵ есть полутоновый интервал вверх;

6)     шестая квинта  2¹⁰/3⁶, как мы уже знаем, означает обращённый три­тон.    

Ступень 2²/3 с №13 фа^Δ (3¹²/2¹⁹) даёт новый разностный интервал  3¹³/2²¹  - это есть кварта, уменьшенная на Δ (фа^Δ-ля^#);

   интервал 2³/3² даёт новый с №13 фа^Δ интервал, равный 3¹⁴/2²²  - целый тон, увеличенный на Δ (ре^#-фа^Δ);

    - " - 2⁵/3³ с той же ступенью №13  образует новую разность 3¹⁵/2²⁴ или малую терцию, уменьшенную на Δ (фа^Δ-соль^#);

     - " - 2⁶/3⁴ образует с №13 интервал 3¹⁶/2²⁵ – большую терцию, увели­ченную на Δ (до^#-фа^Δ);

     - " - 2⁸/3⁵ даёт  интервал 3¹⁷/2²⁷ -  «уменьшенный полутон» (фа^Δ-фа^#);

     - " - ступень 2¹⁰/3⁶, т.е. си^Δ- даёт с фа^Δ+  новый разностный ин­тервал 3¹⁸/2²⁹, который, очевидно, есть уже интервал тритона, уменьшенного на 2Δ (фа^Δ+-си^Δ-).

 

         Обра­зование каждого нового интервала  всегда определено иным показателем степени 3ⁿ и не зависит от показателя степени 2^m. Точно так не кажется неожиданным, что число возможных интервалов между двумя данными ступенями  не превышает разности номеров образующих эти ступени квинт, - то есть разности показателей степени n или  частного от деления  чисел ступеней. Поэтому в дальнейшем мы будем указывать  величину ступени и интервала одним лишь этим  показателем степени n. Номер образующей квинты полностью характеризует данную ступень и связанный с ней интервал,  определяя  её координату - «квинтовое расстояние» от единичной ступени  3⁰ (фа №1), или же соответ­ствующее этому интервалу «расстояние» между  произвольными ступенями.  «Квинтовые расстояния» фрактальны‚ поскольку каждый новый их период то складывается‚ то вычитается с предыдущим‚ но порождаемые ими циклы и паттерны‚ как мы сейчас увидим‚ совершенно регулярны.

Точно так должно быть ясным, что две разные ступени, характери­зуемые каждая своим номером или «квинтовым расстоянием» от 1, а также и два интервала с различными показателями n никогда не совпадают: 3 и 2 взаимно простые числа, отсюда следует‚ что 3ⁿ и 2^m неравны при любых n и m‚ а   и     неравны между собой‚ если   n₁¹ n₂  и  m₁¹ m₂.

Вся эта система впечатляет совершенной регулярностью‚ являя для любого непредубеждённого взгляда свидетельство абсолютной математической строгости квинтовой системы. Не имеет значения, что для музыкальной теории появление комматически изме­нённых интервалов уже более трёх столетий служит лишь вящим доказательст­вом «непригодности» квинтового строя. Музыка‚ как  в этом нетрудно убедиться‚ по природе своей близка «матерям» - подсознательному, законам числа и  времени,  - и ни в малой мере не есть результат со­глашения (конвенции) или набор произвольных  правил.

Иное дело, что внутренние потребности, развиваемые западноевропейской музыкой, шли вразрез с объективно суще­ствующими прогрессиями «реальной гармонии» - или, сказать лучше, для её  музыкальной практики были значимы лишь «отношения I порядка» – а именно те, что задаются  пер­выми  12-ю  ступенями.

Комма была воспринята как нежелательная («13-я» в круге квинт), и стимулировала поиски замкнутой музыкальной системы (в которой бы конец в точности совпадал с началом). В натуре октавы было «загибаться», рационалистический XVII век решил выпрямить её.

Как здесь не привести слова Алистера Кроули:

 

                     «Своей слепотой по всем красотам и чудесам Вселенной человечество обязано иллюзии прямоты»[12].

 

Головокружительный успех темперированного строя – всей европейской классика начиная от И.-С. Баха – привёл к «частичной амнезии»  относи­тельно природы численных корней музыки. «Полностью уравняв в правах» двенадцать интервалов - про­сто-напросто приписав им значение- новоевропейская музыкальная тео­рия, всё же‚ не могла  не сохранить объяснимый  лишь пифагорейской  «асимметрией» гармонический паттерн – а именно, соотношение белых и чёрных клавиш: 7 основных  ступеней + 5 изменённых = 12 (см. Фиг. 3.11)[13].

  Тем не менее, двенадцать темперированных ступеней заключают архетип Октавы (см. Числа)‚ одновременно совмещая в себе (но лишь идеально!) пифагорейское «Золотое деление» и строгое логарифмическое самоподобие, а потому разработанная на отвлечённых гармо­нических принципах европейская  классика в своих наиболее совершенных образцах могла вплотную приближаться к  «объективному  искус­ству».

 

 Рассмотрим  структуру натурального строя в чисто-числовом ключе - в качестве вполне отвлечённой  модели, имея в виду и тот особый смысл, который вкладывали  в неё древние.

Итак, шесть квинт вверх от  исходного фа порождают семь ступеней октавного деления с пятью целотоновыми и двумя полутоновыми промежут­ками, а равно и шесть основных интервалов, возможных между этими сту­пенями (не считая обращённых, т.е. тех, что дополняют последние до октавы – секст и септим – в 4; 4,5; 5 и 5,5 тона). Продолжение квинт с седьмой по одиннадцатую даёт дополнительно пять полутоновых промежутков или пять изменённых (пониженных на полтона) основных ступеней: всего 12 ступе­ней и 12 возможных интервалов (учитывая приму – единичный интервал вместе с её обращением – самой октавой). 12 полутоновых промежутков между первыми двенадцатью квинтовыми ступенями целиком вошли в современную музы­кальную систему темперированного строя, за исключением всех натуральных гармонических отношений:  в последнем случае октава оказалась разделена на 12 логарифмически  равных интервалов.

   

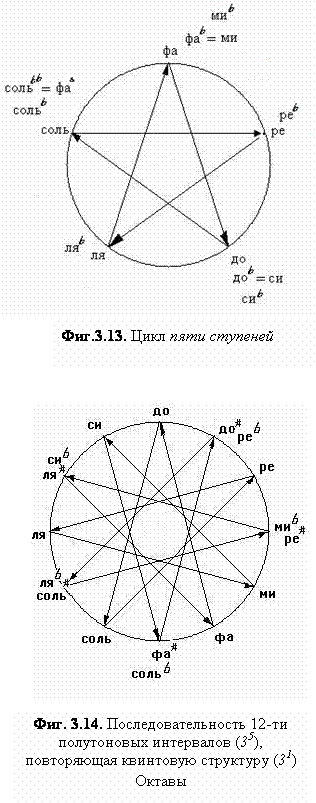
Пульсации чисел октавы следуют определённым ритмам. Роль порож­дающей четверицы или паттерна квинты и кварты была показана нами выше. Следующим обна­руживаемым числовым порядком является  цикл 5-ти. Ступени 1-5 (фа-до-соль-ре-ля) не образуют между собой полутоновых интервалов и задают пентатонику - гамму с интервалами не менее тона (эта сис­тема широко распространена в народной музыке). Все последующие ступени можно представить как повторение этой же последо­вательности с понижением на полтона через каждые пять ступеней (при этом добавляется знак бемоля):  №1фа-№2до-№3соль-№4ре-№5ля-№6ми(=фа^b)-№7си(=до^b)-№8соль^b-№9ре^b-№10ля^b -№11 ми^b(=фа^bb), и т.д.  (Фиг. 3.13.).

При движении против часовой стрелки (понижающимися квинтами) об­ратные циклы приводят к повышению на полтона через каждые пять ступе­ней: ля-ре-соль-до-фа - ля^#-ре^#-соль^#-до^#-фа^# - си^Δ- (=ля^##) -ми^Δ- (=ре^## )‚ и т.д.

 

      Закономерность эта совершенно регулярна и лежит, о чём подробнее ниже, в основании известных со времён бронзы - и дошедших до наших дней - шестидесятиричных циклов (от ки­тайского цикла лет до циферблата наруч­ных часов)[14]. В самом деле, 12 полутоновых интервалов октавного пространства  должны быть покрыты за 12 пятиричных циклов добавления полутона (12 х 5 шагов квинты).

 

Порядки 5-ти и 7-ми  (диатоника) в цикле двенадцати  ступеней определяют‚ как уже отмечено,  важнейшие гармонического свойства музыки.

 

Не может пройти мимо внимания «взаимнооднозначное соответствие» ходов в квинту (3/2) и полутоновых ходов (3⁵/2⁸) в 12-ти ступенном круге. Расположение по квинтам связывает ступени полутоновыми хордами (3⁵)‚ образую­щими  двенадцатиконечную звезду (Фиг. 3.10.б), и точно таким же способом можно представить круг полутоновой гаммы октавы - начальное и конечное до в ней совпадают, и хорды в этом случае соответствуют квинтам - Фиг. 3.14. Отсюда же следует параллель между самим октавным интервалом (до-до¹)  и  микроинтервалом D (№1-№13).

Соответствие полутона и квинты   повторяет изна­чальный паттерн тетрактиды,  порождающей  деление целого тона. Полутон (3⁵) и «увеличенный полу­тон» (3⁷) делят  тоновый интервал  с образованием микротона D посередине подобно тому, как квинта и обращенная квинта (кварта) делят октаву с обра­зованием тонового промежутка - ср. Фиг. 3.2. и  3.15.

 

         Вскоре мы продемонстрируем и другие аналогии  между октавой и целотоновым‚ а также  микротоновыми  делениями‚  циклами 12-ти‚  53-х  и 665-ти ступеней.  Девять микротонов внутри целого тона‚ образованные интервалами D,  и  вложенные паттерны более высоких порядков были известны под наименованием внутренних октав. Термин «внутренняя октава» широко использовался  в школе Г.И. Гурджиева[15].

 

От каждой из семи последовательных квинтовых ступеней‚ если их брать поочерёдно в качестве тоники, можно построить гамму одного из семи параллельных ладов, то есть состоящих из одних и тех же звуков — (2). В этих семиступенных диатониках (пять интервалов целого тона и два интервала полутона семи ступе­ней‚ расположенных в порядке возрас­тания) порядок интервалов циклически меняется (Фиг. 3.3).

 

                               

 

Чередование в цикле 12-ти следует одновременно пятеричному и семеричному паттернам, а своеобразный характер их асимметрии служит образующей для ладов и гармонических структур музыки.  Таким образом, психологические особенности музыкального восприятия также заложены квинтовой последовательностью. В европейской теории отправными служат диатоники двух ладов так называемых натуральных мажора ТТп/тТТТп/т и минора  Тп/тТТп/тТТ.

 Если провести диаметр через любые противоположные позиции 12-ти членного  круга  квинт, как показано  на Фиг. 3.17, то семь ступеней каждой половины круга (включая расположенные на диаметре) дают два набора звуков, слагающих две семиступенные мажорные или минорные гаммы с одним общим звуком (по­скольку через 12 номеров идёт сту­пень, отличающаяся на микротон D  от  исходной).

В каждой семёрке  первая квинтовая ступень является субдоми­нантой, вторая квинтовая ступень – тоникой и третья  – доминантой ма­жорного лада (ТТп/тТТТп/т). Если же в качестве опорного звука - тоники - принять пятую по порядку ступень, получается гамма минорного лада (Тп/тТТп/тТТ), отличающаяся от мажорной на малую терцию (Тп/т) или расстояние в три квинты (четверть окружности).  Субдоминантой в ней будет предшествующая тонике четвёртая‚ а доминантой - следующая за ней шестая ступень. Квинтовый круг показывает известное обратное положение минора в отношении к мажору.

 

 

дальше >>>

 

на главную

 

словарь музыкальных терминов